Расчет газобетонных блоков на дом в онлайн-калькуляторе
Газобетонные блоки относятся к востребованным кладочным материалам, имеющим оптимальные характеристики для частного малоэтажного строительства. Они реализуются на возвратных поддонах с разным объемом, с целью оптимизации затрат на приобретение, доставку и разгрузку важно рассчитать их требуемое число правильно. Упростить эти действия помогают специальные строительные калькуляторы и сервисы поддержки, работа с ними не требует особых навыков и знаний.
Оглавление:
- Необходимость вычислений
- Как пользоваться онлайн-калькулятором?
- Расшифровка результатов
Цели расчета количества газобетона
Блоки из пористых марок легкого бетона характеризуются повышенной геометрической точностью и хорошей способностью к энергосбережению, при необходимости они успешно используются при строительстве несущих вертикальных конструкций с разным функциональным назначением – от наружных стен до внутренних перегородок дома. Несмотря на простые схемы и легкость распила, рассчитывать количество без чертежа крайне сложно, лучшие результаты достигаются при монтаже целых изделий. Это приводит к необходимости задействования специальных графических программ, в точности учитывающих их размеры и подбирающих оптимальные схемы расположения.
Несмотря на простые схемы и легкость распила, рассчитывать количество без чертежа крайне сложно, лучшие результаты достигаются при монтаже целых изделий. Это приводит к необходимости задействования специальных графических программ, в точности учитывающих их размеры и подбирающих оптимальные схемы расположения.
Потребность в таких операциях возникает при самостоятельном проектировании домов из газобетона, расчете для хозпостроек, гаражей, бани или межкомнатных перегородок. Такие сервисы подходят для проверки готовых чертежей или помогают составить новые. При правильном вводе данных они позволяют рассчитать ориентировочное количество для закладки горизонтальных перекрытий, отдельных опор или сплошных ограждений.
Что следует учесть при вводе данных в онлайн-калькулятор?
Исходными параметрами служат размеры элементов (длина, ширина и толщина), марка плотности, общий периметр постройки и средняя высота стен. Правильный калькулятор позволяет рассчитать количество с учетом дверных и оконных проемов, толщины шва (при отсутствии такой графы монтаж газобетонных блоков ведется на клей в пределах 1-3 мм, не более), наличия и вида армосетки. Размерные характеристики вводятся с точностью до мм, длину стен указывают в м, площадь проемов – в м2. Единицы измерения при внесении данных могут отличаться, этот этап требует особого внимания.
Правильный калькулятор позволяет рассчитать количество с учетом дверных и оконных проемов, толщины шва (при отсутствии такой графы монтаж газобетонных блоков ведется на клей в пределах 1-3 мм, не более), наличия и вида армосетки. Размерные характеристики вводятся с точностью до мм, длину стен указывают в м, площадь проемов – в м2. Единицы измерения при внесении данных могут отличаться, этот этап требует особого внимания.
Требуемая схема учитывается в онлайн-калькуляторе в графе «толщина стен», выбирается монтаж в 0,5, 1, 1,5 или 2 газоблока, ее придерживаются в ходе дальнейшего строительства. Избежать ошибок помогает ее графическое изображение. При пропускании или игнорировании какой-либо графы программа не запустится или проведет расчет по стандартным значениям. По умолчанию онлайн-калькулятор строительства дома считает изделия для однорядной кладки с классической перевязкой. Итоговая толщина получаемых стен в этом случае равняется половине элемента (т.е. его ширине).
Количество материала для перегородок и внутренних конструкций рассчитывается отдельно, с полным вводом и проверкой исходных данных. Схема выбирается по умолчанию. Отдельный расчет газобетона проводится также при комбинировании изделий с разными размерами (или при необходимости – с отличающимися марками плотности), свой для каждого участка. Данный способ позволяет получить точную смету на каждую разновидность блоков, но следует помнить, что они будут упакованы на разных поддонах. Все значения вводятся в графы в целом виде (исключение делается для периметра возводимых стен, его величину разрешают задавать черед точку), с учетом рекомендаций разработчика сервиса.
Схема выбирается по умолчанию. Отдельный расчет газобетона проводится также при комбинировании изделий с разными размерами (или при необходимости – с отличающимися марками плотности), свой для каждого участка. Данный способ позволяет получить точную смету на каждую разновидность блоков, но следует помнить, что они будут упакованы на разных поддонах. Все значения вводятся в графы в целом виде (исключение делается для периметра возводимых стен, его величину разрешают задавать черед точку), с учетом рекомендаций разработчика сервиса.
Калькулятор запускается после визуальной проверки данных путем нажатия плунжера, с целью исключения ошибок расчет можно продублировать и повторить.
Как пользоваться результатами онлайн-сервиса?
Стандартный строительный калькулятор помогает получить:
- Общее количество элементов для возведения конструкций.
- Их вес без влияния раствора и армирования.
- Объем клеевой смеси или ЦПР для монтажа блоков газобетона.
 Эта величина является усредненной и действует при использовании в ходе замеса классических пропорций.
Эта величина является усредненной и действует при использовании в ходе замеса классических пропорций. - Число рядов кладки на каждый участок с отдельно заданной высотой.
- Метраж армирующей сетки.
- Ориентировочную нагрузку коробки на основание.
Также с его помощью проверяется длина и общая площадь возводимых конструкций и рассчитывается ширина стены с учетом выбранной схемы и толщины швов. Полученные данные носят рекомендательный характер и используются при покупке стройматериалов в ходе постройки дома из газобетона. Они не учитывают потерь при транспортировке и разгрузке, перерасхода или выбрасываемых остатков клеевой смеси, обусловленных неопытностью работников или других возможных случаев выбраковки. Рекомендуемая минимальная величина запаса для кладочных материалов составляет 5 %, клеевых смесей – 10. Округление результатов расчета количества блоков проводится исключительно в большую сторону.
Строительный калькулятор | Комбинат пористых материалов
Пазогребневые газобетонные блоки автоклавной обработки производятся на оборудовании и по технологии немецкой фирмы WEHRHAHN в соответствии с ГОСТ 31359-2007, ГОСТ 31360-2007.
Оформить заказ
Скачать прайс
625
100
250
93,75 c/шт
Масса блока — до 9,8 кг*
В поддоне — 96 шт, 1,5 м3
Зависит от плотности
625
200
250
187,50 c/шт
Масса блока — до 19,5 кг*
В поддоне — 48 шт, 1,5 м3
Зависит от плотности
625
300
250
281,25 c/шт
Масса блока — до 29,2 кг*
В поддоне — 32 шт, 1,5 м3
Зависит от плотности
625
400
250
375,00 c/шт
Масса блока — до 39 кг*
В поддоне — 24 шт, 1,5 м3
Зависит от плотности
за м3
6000 c
поддон 1,5 м3
9000,00 c
При покупке больших объемов мы предоставим вам скидку.
Наружные стены
Внутренние перегородки
Этаж
1
Толщина блока, мм
ГБ-1 (100)ГБ-2 (200)ГБ-3 (300)ГБ-4 (400)
Высота стен, м
Периметр стен, м
Площадь проемов, м2
Необходимо материалов
на этаж
Поддоны, шт:
0
Блоков, м30
Клей, мешков
0
Добавить этаж
Этаж
1
Толщина блока, мм
ГБ-1 (100)ГБ-2 (200)ГБ-3 (300)ГБ-4 (400)
Высота стен, м
Сумма перегородок, м
Площадь проемов, м2
Необходимо материалов
на этаж
Поддоны, шт:
0
Блоков, м30
Клей, мешков
0
Добавить этаж
Область применения:
- Внутренние перегородки в жилых и общественных зданиях (ГБ1 и ГБ2).

- Несущие конструкции и стены в малоэтажном строительстве до 3-х этажей (ГБ2, ГБ3 и ГБ4).
- Наружные стены в монолитном и монолитно-каркасном строительстве – независимо от высотности (ГБ2, ГБ3 и ГБ4).
На заказ можем произвести блоки без пазогребневой конструкции шириной 150 мм.
Пазогребневая конструкция предотвращает появление «мостиков холода».
Легко сверлить, пилить, фрезеровать и забивать гвозди. Сборка конструкций в 5 раз быстрее.
Выдерживает большие нагрузки благодаря автоклавной обработке (не менее 35 гс/см2).
Технические характеристики
| Плотность в сухом состоянии | 400 кг/м3 | 500 кг/м3 | 600 кг/м3 |
| Класс прочности | 1,5-2,5 | 2,5-3,5 | 3,5 |
| Марка прочности на сжатие | м25-35 | м35-50 | м50 |
| Теплопроводимость в сухом состоянии | 0,08 вт/м с | 0,12 вт/м с | 0,13 вт/м с |
| Марка по морозостойкости | — | F 150 | F 150 |
| Паропроницаемость | 0,27 мг/м. ч.па ч.па | 0,20 мг/м.ч.па | 0,20 мг/м.ч.па |
| Отпускная влажность | < 35% | < 35% | < 30% |
| Усадка при высыхании | — | 0,4 мм/м | 0,4 мм/м |
| Класс радиоактивности | первый | первый | первый |
Калькулятор закона идеального газа (давление–объем–температура–количество) • Термодинамика — теплота • Онлайн-конвертеры единиц измерения
Этот калькулятор закона идеального газа определяет одно из четырех значений в уравнении идеального газа (давление, объем, температура или количество), если известны еще три.
Пример: Рассчитайте давление в паскалях 800 моль метана, хранящегося при 30 °C в 70-литровом баке автомобиля, работающего на метане.
Больше примеров задач уравнения идеального газа и их решения вы найдете под калькулятором.
Выберите «Неизвестное», чтобы решить уравнение идеального газа:
P V T N
Absolute Diface
0009
Absolute Dampail 9000
9000.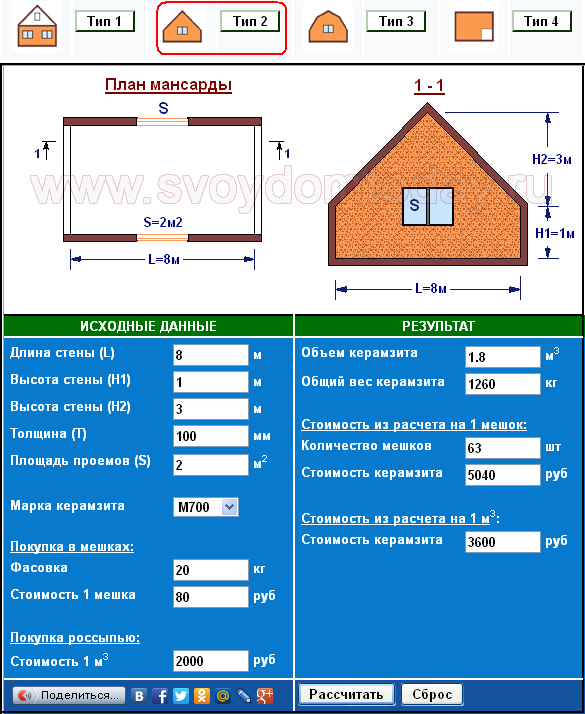 LASPARS (PAGARSMAST 9000AST
LASPARS (PAGARSMAST 9000AST
9000. (МПа)килопаскаль (кПа)гектопаскаль (гПа)ньютон/метр² (Н/м²)бар (бар)килограмм-сила/метр² (кгс/м²)торр (торр)psi (psi)миллиметр ртутного столба (0°C) (мм рт.ст. )мм водяного столба (4°C) (мм вод. ст.)атмосфера техническая (ат)стандартная атмосфера (атм)
Объем
В метр³ (м³)дециметр³ (дм³)сантиметр³ (см³)литр (л)миллилитр (мл)галлон (США) (гал)кварт (США) (кварт)жидкая унция (США) ( жидкие унции)жидкие унции (Великобритания) (жидкие унции)фут³ (фут³)дюйм³ (дюйм³)
Температура
T градус Цельсия (°C)градус Фаренгейта (°F)градус Ренкина (°R)кельвин ( K)
Количество в молях
n моль
ИЛИ
Молярная масса
M грамм на моль (г/моль) килограмм на моль (кг/моль)
Масса
m миллиграмм (мг) грамм (г) килограмм (кг) унция (унция) фунт (фунт) )
Share
Для расчета выберите неизвестное значение и введите три известных из четырех доступных значений (давление, объем, температура и количество). Нажмите кнопку Calculate , чтобы вычислить неизвестное значение. Вы можете ввести количество в молях или в виде комбинации молярной массы и массы газа. Используйте наш калькулятор молярной массы, чтобы определить молярную массу любого газа. Если вы хотите определить молярную массу смеси газов, например сухого воздуха, вам необходимо определить молярные массы каждого газа и умножить их на мольные доли каждого газа.
Нажмите кнопку Calculate , чтобы вычислить неизвестное значение. Вы можете ввести количество в молях или в виде комбинации молярной массы и массы газа. Используйте наш калькулятор молярной массы, чтобы определить молярную массу любого газа. Если вы хотите определить молярную массу смеси газов, например сухого воздуха, вам необходимо определить молярные массы каждого газа и умножить их на мольные доли каждого газа.
Практические задачи с идеальным газом
Определения и формулы
Идеальный газ
Закон об идеальном газе
Закон Бойля ( T=const, n=const )
Pconst 90)
Закон Шарля ( P=const, n=const )
Закон Гей-Люссака ( V=const, n=const )
Практические задачи с идеальным газом
50 Задача 0 6: При нормальных условиях 0 °С и абсолютное атмосферное давление 100 кПа), плотность воздуха 1,28 кг/м³. Определить среднюю молярную массу воздуха.
Решение: Из данной плотности воздуха мы знаем, что масса одного кубического метра воздуха равна 1,28 кг. Нажмите кнопку Сбросить и введите данные проблемы в калькулятор:
Нажмите кнопку Сбросить и введите данные проблемы в калькулятор:
- Выберите n (Количество в молях) в селекторе Выберите неизвестный .
- Введите абсолютное давление P = 100 кПа.
- Введите объем V = 1 м³.
- Введите температуру T = 0 °C.
- Щелкните или нажмите кнопку Вычислить 9кнопка 0006.
- Будет рассчитано количество 1 м 3 воздуха в молях.
- Введите массу m = 1,28 кг и щелкните или нажмите кнопку Рассчитать .
- Будет рассчитана молярная масса воздуха M = 0,029 кг/моль
Задача 2: Молярная масса газообразного кислорода (O₂) равна M = 32 г/моль. Определить абсолютную температуру 128 г кислорода в 4-литровом сосуде при давлении Р = 3 МПа.
Решение: Нажмите кнопку Сброс и введите данные о проблеме в калькулятор:
- Выберите T (Температура) в селекторе Выберите неизвестный селектор.
- Введите молярную массу кислорода M = 32 г/моль.

- Введите массу кислорода m = 128 г.
- Будет рассчитано количество кислорода в молях.
- Введите объем V = 4 л и давление P = 3 МПа.
- Щелкните или нажмите кнопку Вычислить .
- Считайте температуру в кельвинах.
Задача 3: Сосуд высокого давления заполнен газом с давлением P = 0,5 МПа и температурой T = 15 °C. Объем газа V = 5 л. Рассчитайте объем этой массы газа при нормальных условиях (P = 100 кПа, T = 0 °С).
Решение: Нажмите кнопку Сбросить и введите данные проблемы в калькулятор:
- Выберите n (Количество в молях) в Выберите неизвестный селектор .
- Введите давление P = 500 кПа.
- Введите температуру T = 15 °C.
- Введите объем V = 5 л.
- Щелкните или нажмите кнопку Рассчитать .
- Калькулятор рассчитает количество в молях, которое будет использовано позже.
- Изменить Выберите неизвестный селектор на Volume .

- Введите давление и температуру для нормальных условий P = 100 кПа, T = 0 °C и щелкните или нажмите кнопку Кнопка «Рассчитать «.
- Будет рассчитан объем V = 23,69 л при нормальных условиях.
Задача 4: Рассчитайте давление в паскалях 12,8 кг метана (молекулярная масса 16 г/моль), хранящегося при 30 °C в 70-литровом баке автомобиля, работающего на метане.
Определения и формулы
Идеальный газ
Идеальный газ — это теоретическая модель газа, в которой газ представлен множеством случайно движущихся точечных частиц, которые взаимодействуют друг с другом только идеально упруго, то есть при столкновении двух частиц, их кинетическая энергия остается неизменной и не преобразуется ни в какую другую форму энергии, такую как потенциальная энергия или теплота. Частицы газа называются точечными, потому что предполагается, что они не занимают никакого пространства. Эта теоретическая модель полезна, поскольку упрощает многие расчеты и потому, что идеальный газ подчиняется законам Ньютона. Его можно представить себе как совокупность совершенно твердых сфер, которые сталкиваются и никак иначе не взаимодействуют друг с другом.
Его можно представить себе как совокупность совершенно твердых сфер, которые сталкиваются и никак иначе не взаимодействуют друг с другом.
В обычных условиях, таких как стандартные условия (температура 273,15 К и давление 1 стандартная атмосфера), большинство реальных газов ведут себя как идеальные газы. Вообще говоря, газ ведет себя как идеальный газ при более низком давлении и более высоких температурах, когда расстояния между молекулами газа относительно велики. В этих условиях потенциальная энергия за счет межмолекулярных сил много меньше кинетической энергии частиц. Размер молекул также незначителен по сравнению с расстоянием между ними. При более низких температурах и более высоких давлениях, а также для тяжелых газов модель идеального газа не работает. Когда температура становится еще ниже, а давление выше, реальный газ может стать жидким или даже твердым, т. е. претерпевать фазовый переход. В то же время модель идеального газа не допускает жидкого или твердого состояния.
Закон идеального газа
Идеальный газ, как и любой газ, можно охарактеризовать четырьмя переменными и одной константой. These are:
- pressure ( P ),
- volume ( V ),
- quantity in moles ( n ),
- temperature ( T ), and
- gas constant ( R )
Эти четыре переменные и одна константа объединены в следующем уравнении, которое называется законом идеального газа :
Это уравнение также известно как уравнение Клапейрона, поскольку оно было впервые сформулировано в 1834 году французским инженером Эмилем Клапейроном (1799–1864). В этом уравнении:
- P — это абсолютное давление, измеренное в СИ в паскалях (Па),
- V — это объем, измеренный в СИ в кубических метрах (м³),
5 — это
4 количество вещества (газа) в молях (моль). Один моль любого соединения, измеренный в граммах, численно равен средней массе одной молекулы соединения в единых атомных единицах массы.
 Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра.
Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра.- T — это абсолютная температура.
- R — газовая постоянная . , также называемая идеальной, молярной или универсальной газовой постоянной, — физическая константа пропорциональности уравнения идеального газа.
Приведенное выше уравнение показывает, что для нулевой абсолютной температуры существует нулевой объем. Однако это не означает, что объем реального газа действительно исчезает. При очень низких температурах все газы становятся жидкостями, а уравнение идеального газа к жидкостям неприменимо.
Газовая постоянная соответствует работе, которую совершает один моль идеального газа при нагревании на 1 К при постоянном давлении. Его размерность — это работа на количество на температуру, а константа точно определена как 8,31446261815324 Дж⋅К⁻¹⋅моль⁻¹. Газовая постоянная также определяется как постоянная Авогадро N A , умноженная на постоянную Больцмана k :
Постоянная идеального газа была открыта и введена в закон идеального газа вместо многих конкретных газовых постоянных Дмитрием Менделеева в 1877 г. Поэтому уравнение закона идеального газа иногда, особенно в русскоязычных учебниках, называют уравнением Менделеева-Клапейрона.
Поэтому уравнение закона идеального газа иногда, особенно в русскоязычных учебниках, называют уравнением Менделеева-Клапейрона.
Химическое количество газа в молях иногда удобнее заменить указанием массы газа. Химическое количество газа в молях n , его масса m в граммах и его молярная масса M в граммах на моль получаются как
. Уравнение газового закона выше, мы получаем:
Чтобы определить молярную массу элемента, его относительную атомную массу умножают на константу молярной массы в кг/моль
Например, молярная масса элементарного кислорода в единицах СИ равна
Теперь, вводя плотность ρ = m/V , получаем:
Теперь введем удельную газовую постоянную как отношение газовой постоянной R к молярной массе M :
Например, удельная газовая постоянная сухого воздуха приблизительно равна 287 Дж·кг⁻¹·K⁻¹. Переписав уравнение идеального газа с использованием удельной газовой постоянной, получим:
Закон идеального газа объединяет четыре эмпирических простых закона газа, открытых несколькими учеными, которые тщательно измеряли свойства газа в 17-19 веках.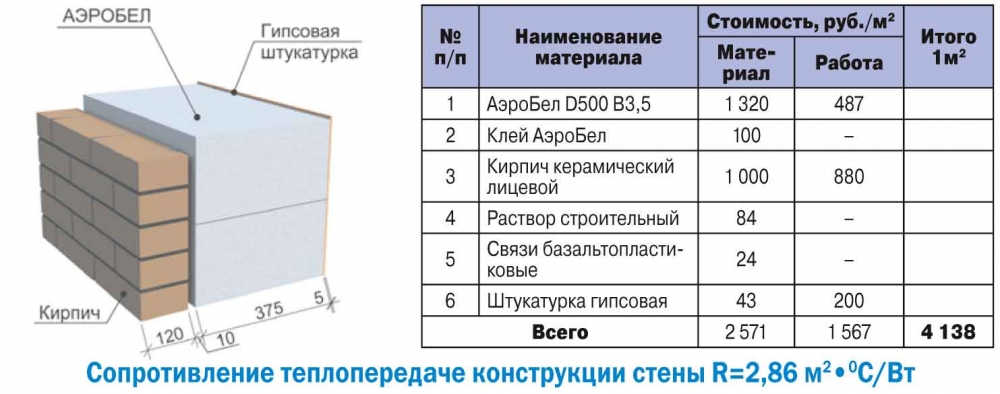 Законы простого газа можно вывести из приведенного выше уравнения идеального газа ( PV=nRT ). Поскольку в этом уравнении R является константой, мы можем написать
Законы простого газа можно вывести из приведенного выше уравнения идеального газа ( PV=nRT ). Поскольку в этом уравнении R является константой, мы можем написать
Поскольку PV/NT является константой, мы можем переписать это в виде: и конечные состояния газа в системе. Мы будем использовать это уравнение ниже для описания четырех газовых законов.
Обратите внимание, что исторически эмпирические газовые законы, описанные ниже, привели к выводу идеального газового закона. Эти законы были открыты несколькими учеными, которые проводили эксперименты, в которых изменялись только две переменные состояния газа, а две другие оставались постоянными.
Закон Бойля (
T=const, n=const )
Роберт Бойль
Теперь, для приведенного выше уравнения, для фиксированного количества газа в молях n при постоянной температуре T мы получаем
или
Edme Mariotte
Это Закон Бойла , в котором описывается взаимосвязь между томом V и давлением P фиксированного количества газа в Moles N AT постоянной температуры . Т . При изменении объема и давления изменение давления обратно пропорционально изменению объема газа. Он был сформулирован англо-ирландским химиком и физиком Робертом Бойлем в 1662 г. В России и континентальной Европе этот закон называют законом Бойля-Мариотта в знак признания вклада французского физика и священника Эдма Мариотта в открытие этого закона.
Т . При изменении объема и давления изменение давления обратно пропорционально изменению объема газа. Он был сформулирован англо-ирландским химиком и физиком Робертом Бойлем в 1662 г. В России и континентальной Европе этот закон называют законом Бойля-Мариотта в знак признания вклада французского физика и священника Эдма Мариотта в открытие этого закона.
Закон Авогадро (
T=const, P=const )
Амедео Авогадро
Если температура и давление постоянны, то мы можем написать
и давление, равные объемы всех газов содержат одинаковое количество молекул. Это уравнение показывает, что если количество газа увеличивается, объем газа увеличивается пропорционально. Другими словами, количество атомов или молекул газа не зависит от их размеров или молекулярной массы газа. Закон назван в честь итальянского ученого Амедео Авогадро, опубликовавшего свою гипотезу о зависимости между объемом газа и его количеством в молях в 1811 году. Его имя носит и постоянная Авогадро.
Закон Шарля (
P=const, n=const )
Жак Шарль
Для фиксированного количества газа в молях, когда его давление поддерживается постоянным, объем газа в системе прямо пропорционален абсолютному температура системы или
Этот закон также называют законом объемов . Проще говоря, закон Шарля описывает, что любой газ расширяется, когда его абсолютная температура увеличивается. Закон был сформулирован в неопубликованной работе французского ученого Жака Шарля в 1780-х годах. Французский химик и физик Жозеф Луи Гей-Люссак опубликовал этот закон в 1803 году и приписал открытие Жаку Шарлю. Поэтому этот закон иногда можно назвать законом Гей-Люссака. Например, в российских учебниках этот закон называется законом Гей-Люссака (русский: закон Гей-Люссака), а итальянские ученые называют его первым законом Гей-Люссака (итал. prima legge di Gay-Lussac).
Закон Гей-Люссака (
V=const, n=const )
Жозеф-Луи Гей-Люссак
Закон Гей-Люссака или закон давления-температуры утверждает, что давление данного количества газа в молях, если его объем постоянен, прямо пропорционален абсолютной температуре газа:
Закон сформулирован Гей-Люссаком в 1802 году. В разных странах этот закон также называют законом Амонтона, потому что его открыл французский ученый Гийом Амонтон. закон на 100 лет раньше Гей-Люссака и описал его количественно. Иногда этот закон называют вторым законом Гей-Люссака и законом Шарля, потому что сам Гей-Люссак считал, что закон был открыт Шарлем. Закон давления-температуры был также независимо открыт английским химиком и физиком Джоном Дальтоном в 1801 году. аналогичные исследования и получили те же результаты.
В разных странах этот закон также называют законом Амонтона, потому что его открыл французский ученый Гийом Амонтон. закон на 100 лет раньше Гей-Люссака и описал его количественно. Иногда этот закон называют вторым законом Гей-Люссака и законом Шарля, потому что сам Гей-Люссак считал, что закон был открыт Шарлем. Закон давления-температуры был также независимо открыт английским химиком и физиком Джоном Дальтоном в 1801 году. аналогичные исследования и получили те же результаты.
По мере того, как воздух в оболочке воздушного шара нагревается, его плотность становится меньше, чем у наружного воздуха, что делает воздушный шар плавучим.
Эта статья была написана Анатолием Золотковым
Калькулятор объема
Ниже приведен список калькуляторов объема для нескольких распространенных форм. Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор кубического объема
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
|
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.
|
Калькулятор объема усеченного конуса
|
Калькулятор объема эллипсоида
|
Калькулятор объема квадратной пирамиды
Калькулятор объема пробирки
|
Связанные Калькулятор площади поверхности | Калькулятор площади
Объем – это количественная оценка трехмерного пространства, занимаемого веществом. Единицей объема в СИ является кубический метр, или м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы. Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Единицей объема в СИ является кубический метр, или м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы. Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, равноудаленных от данной точки в его центре, где расстояние между центром и любой точкой на сфере равно радиусу r . Вероятно, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и вычисление их объемов одинаково. Как и в случае с окружностью, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром, д . Уравнение для расчета объема сферы приведено ниже:
| объем = | πr 3 |
EX: Клэр хочет наполнить уксусом идеально сферический водяной шар радиусом 0,15 фута, чтобы использовать его в битве с водяным шаром против ее заклятого врага Хильды в ближайшие выходные. Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:
Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус представляет собой трехмерную форму, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован подобно кругу набором отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или какое-либо другое основание). На этой странице рассматривается только случай конечного прямого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. д., которые простираются до бесконечности, рассматриваться не будут. Уравнение для расчета объема конуса выглядит следующим образом:
| объем = | πr 2 ч |
где r — радиус, а h — высота конуса
ПРИМЕР: Беа полна решимости выйти из магазина мороженого с хорошо потраченными 5 долларами, заработанными тяжелым трудом. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее. Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:
Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее. Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйма 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет < 15%, и решает купить сахарный рожок. . Теперь все, что ей нужно сделать, это использовать свою ангельскую детскую привлекательность, чтобы заставить персонал опустошить контейнеры с мороженым в ее рожок.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых сходятся в каждой из его вершин и все перпендикулярны соответствующим смежным граням. Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр. Ниже приведено уравнение для расчета объема куба:
Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр. Ниже приведено уравнение для расчета объема куба:
объем = а 3
где a — длина ребра куба
ПРИМЕР: Боб, родившийся в Вайоминге (и никогда не покидавший штат), недавно посетил родину своих предков в Небраске. Потрясенный великолепием Небраски и окружающей средой, непохожей ни на что другое, с чем он когда-либо сталкивался ранее, Боб понял, что ему нужно привезти часть Небраски домой с собой. У Боба есть кубический чемодан с длиной ребра 2 фута, и он вычисляет объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от заданной прямой оси. Однако в обычном употреблении «цилиндр» относится к прямолинейному круговому цилиндру, основаниями которого являются окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . . Уравнение для расчета объема цилиндра показано ниже:
. Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
ПРИМЕР: Кэлум хочет построить замок из песка в гостиной своего дома. Поскольку он решительно выступает за переработку отходов, он нашел три цилиндрические бочки с незаконной свалки и очистил их от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя приведенное ниже уравнение:
объем = π × 3 2 × 4 = 113,097 фута 3
Он успешно строит замок из песка в своем доме и, в качестве дополнительного бонуса, ему удается экономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте. темнота.
Прямоугольный резервуар
Прямоугольный резервуар представляет собой обобщенную форму куба, стороны которого могут иметь различную длину. Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем= длина × ширина × высота
ПРИМЕР: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к тортам. Она планирует пройти по тропе Калалау на Кауаи, и, хотя Дарби в отличной форме, она беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет наполнить свой идеально прямоугольный пакет длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитывается ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула представляет собой трехмерную геометрическую форму, состоящую из цилиндра и двух полусферических концов, где полусфера представляет собой половину сферы.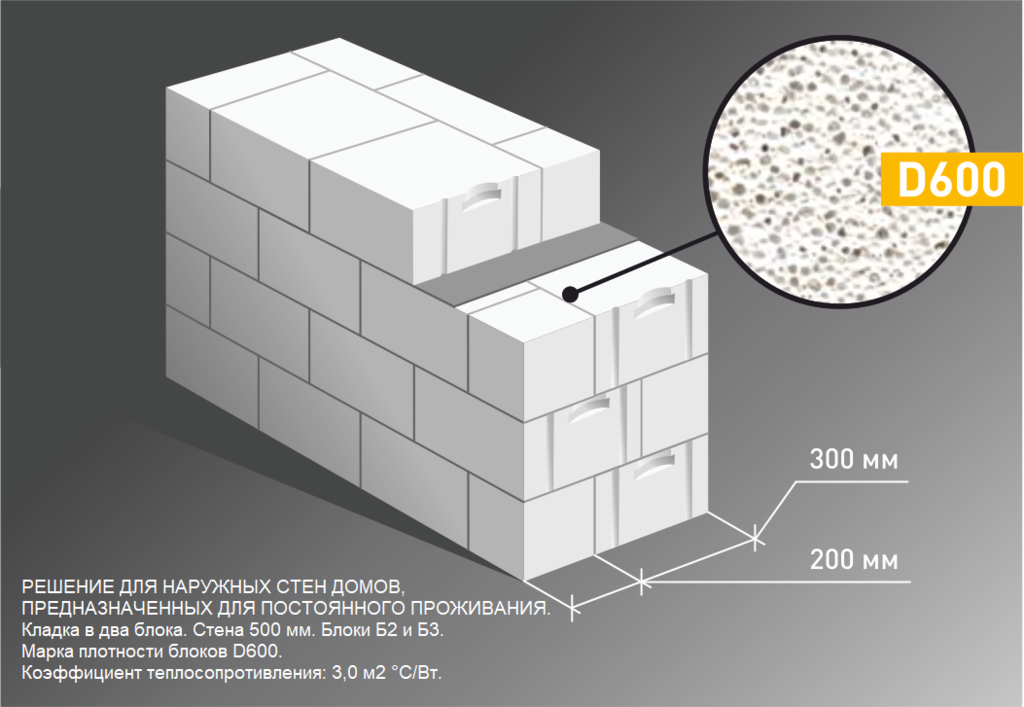 Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:
Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + ч) |
где r — радиус, а h — высота цилиндрической части
ПРИМЕР: Дана капсула с радиусом 1,5 фута и высотой 3 фута. Джо может взять с собой капсулу времени, которую он хочет закопать для будущих поколений в своем путешествии самопознания через Гималаи:
объем = π × 1,5 2 × 3 + 4/3 ×π ×1,5 3 = 35,343 футов 3
Сферическая крышка
Сферическая крышка представляет собой часть сферы, отделенную от остальной части сферы плоскостью. Если плоскость проходит через центр сферы, сферическая шапка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера разделена на две параллельные плоскости и два разных радиуса, где плоскости проходят через сферу. Уравнение для расчета объема сферической шапки получено из уравнения для сферического сегмента, где второй радиус равен 0. Относительно сферической шапки, показанной в калькуляторе:
Уравнение для расчета объема сферической шапки получено из уравнения для сферического сегмента, где второй радиус равен 0. Относительно сферической шапки, показанной в калькуляторе:
| объем = | πh 2 (3R — h) |
Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Данный R и R : H = R ± √r 2 — R 2
| дано R и H : R = |
|
 Эта величина является усредненной и действует при использовании в ходе замеса классических пропорций.
Эта величина является усредненной и действует при использовании в ходе замеса классических пропорций.
 Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра.
Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра. Он отрезает идеальный сферический колпачок от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:0003
Он отрезает идеальный сферический колпачок от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:0003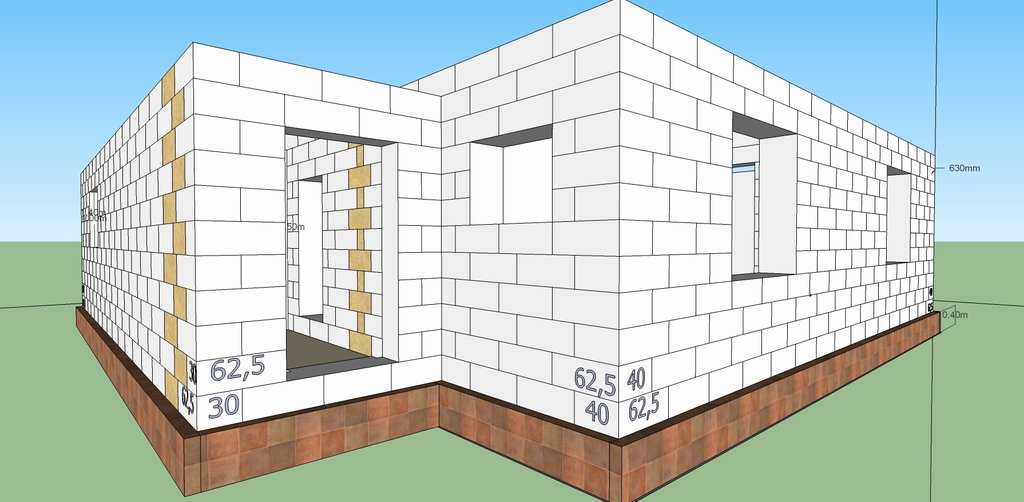 Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с протекающим мороженым в правом коническом усеченном конусе, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:
Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с протекающим мороженым в правом коническом усеченном конусе, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма: Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:
Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом: Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:
Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида: С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже: