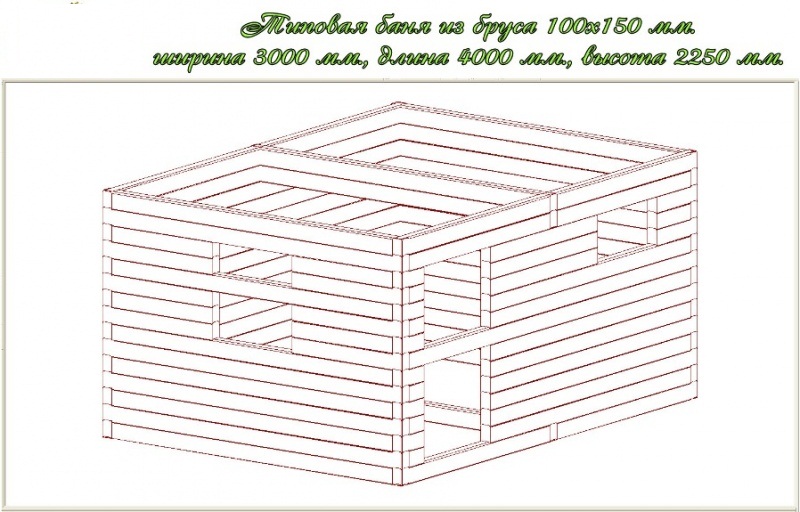
Онлайн калькулятор сруба из бруса: Онлайн калькулятор расчета бруса на дом и баню

Калькулятор сруба

Конструктор сруба (колодца)

С помощью калькулятора вы имеете возможность рассчитать примерную стоимость сруба по целому ряду параметров: основным габаритам строения, фундамента, кровли, полов, потолков, способов обработки древесины…

Подчеркиваем: данный расчет носит лишь предварительный характер. В нем не учитываются инженерные коммуникации (обустройство электро и водоснабжения, канализации, отопления и пр.) Внутренние отделочные работы также требуют отдельного просчета с учетом утвержденного проекта.

Узнать точную цену Вы можете, отправив нам запрос, либо позвонив в офис компании: +7-988-242-86-66

Введите параметры будущего Вашего дома.

Тип дома




Бревно ручной рубки




Оцилиндрованное бревно




Профилированный брус




Строганный брус

Высота рубленных фронтонов

Ширина сруба

от 1. 5 до 12 метров

Длина сруба

от 1.5 до 12 метров


Высота первого этажа


Высота крыши


Высота сруба второго этажа

Дополнительная стена


По ширине


По длине

Тип рубки


В чашу


В лапу

Диаметр бревна

Сруб: 6×6м в чашу. Диаметр бревна: 22см. Дополнительные стены: нет.

84м²

447 000 руб

Тип крыши, материал и утепление кровли

Тип крыши


Чердачная


Мансардная

Материал кровли


Нет кровли


Рубероид


Металлическая черепица


Мягкая кровля

Утепление кровли


Без утепления


Малый пирог (летний дом)


Полный пирог (зимний дом)

Материал: Стропильная система. Утепление: Без утепления.

69 м²

0 руб

Фундамент

Тип фундамента


Без фундамента


Столбчатый


Свайный


Ленточный (50+50)x30 см

Полы, Потолки

Полы


Без полов


Черновые полы


Чистовые полы

Потолки


Без потолков


С потолками

Отделка: Дополнительные услуги

Дополнительные услуги


Шлифовка внутренняя


Покраска


Биозащита


Огнезащита


Конопатка

Итоговая стоимость 447 000 руб

Калькулятор: расчет количества материалов для сруба из бруса и бревен

РЕЗУЛЬТАТЫ ПОДСЧЕТОВ ПО ЗАДАННЫМ РАЗМЕРАМ

«;
document.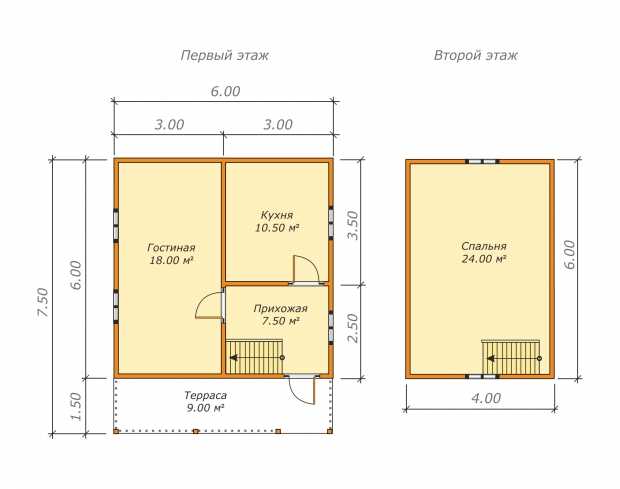 getElementById(‘raschet’).innerHTML += «Объем для строительства сруба со всеми стенами составляет: «+all_info.toFixed(2)+» куб. м.

«;
document.getElementById(‘raschet’).innerHTML += «Для строительства сруба со всеми стенами требуется «+obj_dlina.toFixed(2)+» погонных метров оцилиндрованного бревна/бруса»;
//document.getElementById(‘raschet’).innerHTML += «Количество звеньев дома: «+num_zveno+» шт.
«;
//*******************************************************************
}

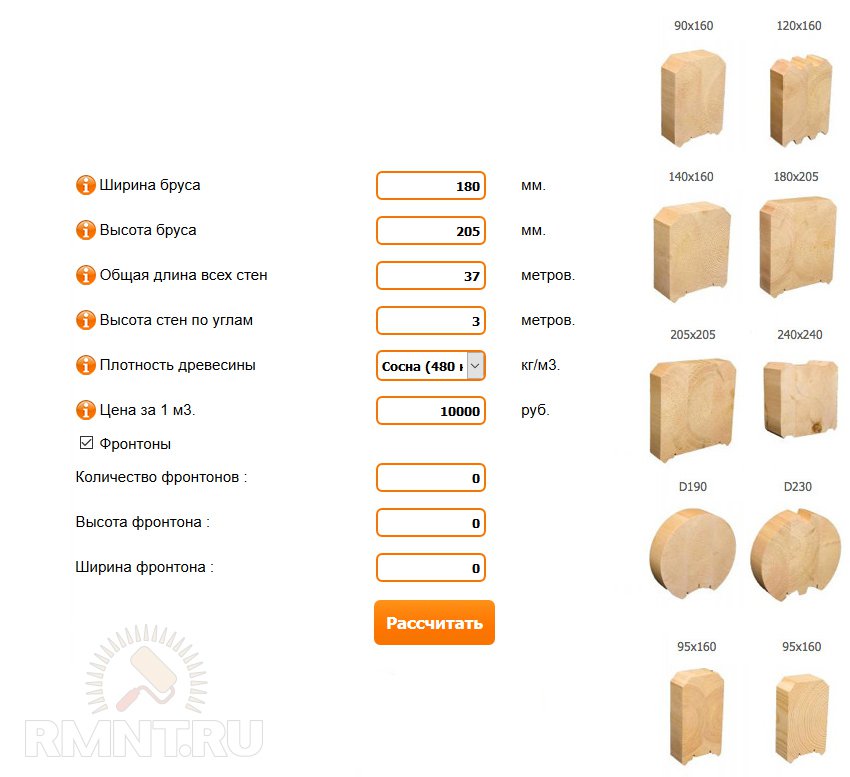
Как рассчитать, сколько потребуется бруса или бревен для строительства сруба? Очень просто — введите требуемые параметры: длину, ширину, высоту сруба, а также данные о внутренних стенах и после заполнения всех нужных полей нажмите кнопку «Рассчитать» в конце калькулятора.

Вниманние! Калькулятор ТОЛЬКО ПРИМЕРНО подсчитывает объем материалов, необходимых для строительства дома. Не учитывается количество окон, дверей и т.п.

—Сруб дома по вашим размерам—
Длина, м3 м.
3.5 м.
4 м.
4.5 м.
5 м.
5.5 м.
6 м.
6.5 м.
7 м.
7.5 м.
8 м.
8.5 м.
9 м.
9.5 м.
10 м.
10.5 м.
11 м.
11.5 м.
12 м.
12.5 м.
13 м.
13.5 м.
14 м.
14.5 м.
15 м.
15.5 м.
16 м.
16.5 м.
17 м.
17.5 м.
Ширина, м3 м.
3.5 м.
4 м.
4.5 м.
5 м.
5.5 м.
6 м.
6.5 м.
7 м.
7.5 м.
8 м.
8.5 м.
9 м.
9.5 м.
10 м.
10.5 м.
11 м.
11.5 м.
12 м.
12.5 м.
13 м.
13.5 м.
14 м.
14.5 м.
15 м.
15.5 м.
16 м.
16.5 м.
17 м.
17.5 м.
Высота, м1.5 м.
1.6 м.
1.7 м.
1.8 м.
1.9 м.
2 м.
2.1 м.
2.2 м.
2.3 м.
2.4 м.
2.5 м.
2.6 м.
2.7 м.
2.8 м.
2.9 м.
3 м.
3.1 м.
3.2 м.
3.3 м.
3.4 м.
——Наличие межкомнатных стен и их размеры——
Длина 1-ой стены, мнет стены
3 м.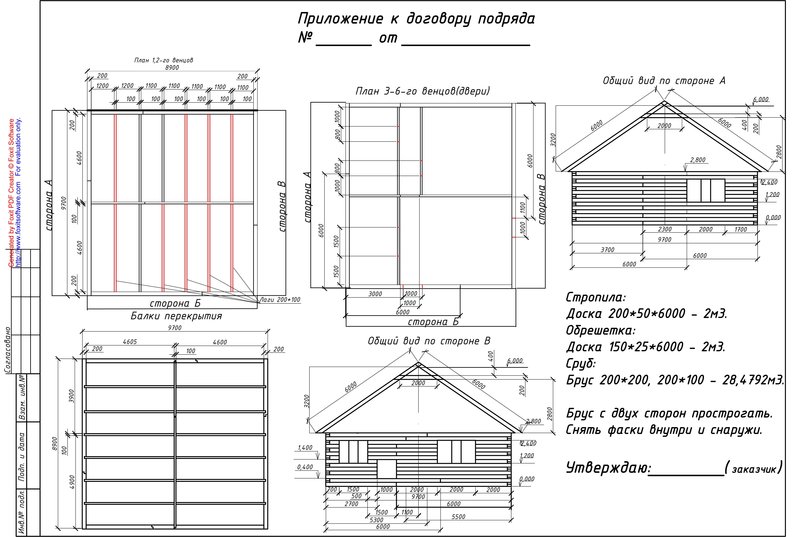
3.5 м.
4 м.
4.5 м.
5 м.
5.5 м.
6 м.
6.5 м.
7 м.
7.5 м.
8 м.
8.5 м.
9 м.
9.5 м.
10 м.
10.5 м.
11 м.
11.5 м.
12 м.
12.5 м.
13 м.
13.5 м.
14 м.
14.5 м.
15 м.
15.5 м.
16 м.
16.5 м.
17 м.
17.5 м.
Длина 2-ой стены, мнет стены
3 м.
3.5 м.
4 м.
4.5 м.
5 м.
5.5 м.
6 м.
6.5 м.
7 м.
7.5 м.
8 м.
8.5 м.
9 м.
9.5 м.
10 м.
10.5 м.
11 м.
11.5 м.
12 м.
12.5 м.
13 м.
13.5 м.
14 м.
14.5 м.
15 м.
15.5 м.
16 м.
16.5 м.
17 м.
17.5 м.
Длина 3-ей стены, мнет стены
3 м.
3.5 м.
4 м.
4.5 м.
5 м.
5.5 м.
6 м.
6.5 м.
7 м.
7.5 м.
8 м.
8.5 м.
9 м.
9.5 м.
10 м.
10.5 м.
11 м.
11.5 м.
12 м.
12.5 м.
13 м.
13.5 м.
14 м.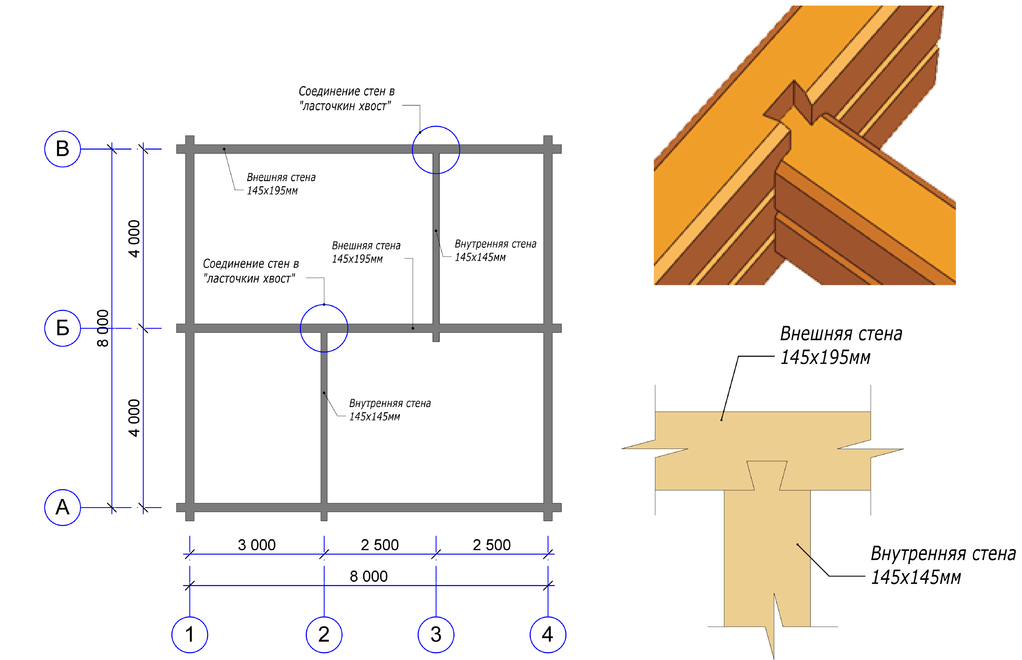
14.5 м.
15 м.
15.5 м.
16 м.
16.5 м.
17 м.
17.5 м.
Длина 4-ой стены, мнет стены
3 м.
3.5 м.
4 м.
4.5 м.
5 м.
5.5 м.
6 м.
6.5 м.
7 м.
7.5 м.
8 м.
8.5 м.
9 м.
9.5 м.
10 м.
10.5 м.
11 м.
11.5 м.
12 м.
12.5 м.
13 м.
13.5 м.
14 м.
14.5 м.
15 м.
15.5 м.
16 м.
16.5 м.
17 м.
17.5 м.
——Используемое бревно/брус при строительстве——
Бревно/брус,мм160 мм.
180 мм.
200 мм.
220 мм.
240 мм.
260 мм.

Заказать строительство дома под ключ или отдельный этап работ можно по тел. (8-909) 155-88-38 или через почтовую форму

См. также:

  • Все строительные калькуляторы
  • Онлайн-проектирование сруба
  • Посчитать количество блоков на дом
  • Строительство дома под ключ
  • Рассчитать количество сайдинга на дом

Эта запись была размещена в Калькуляторы с меткой Брус,Калькуляторы,Сруб.

Roman Chernyshov

Калькулятор логарифмического правдоподобия и величины эффекта

Калькулятор размера выборки — доверительный интервал, доверительный интервал, размер выборки, размер совокупности, релевантная совокупность

Этот калькулятор размера выборки представлен как общедоступная услуга программного обеспечения для проведения опросов Creative Research Systems.
Вы можете использовать его, чтобы определить, сколько людей вам нужно опросить, чтобы получить результаты, отражающие целевую группу настолько точно, насколько это необходимо. Вы также можете найти уровень точности, который у вас есть в существующем образце.

Прежде чем использовать калькулятор объема выборки, необходимо знать два термина. Это: доверительный интервал и доверительный уровень . Если вы не знакомы с этими терминами, нажмите здесь. Чтобы узнать больше о факторах, влияющих на размер доверительных интервалов, нажмите здесь.

Введите свои варианты в калькулятор ниже, чтобы найти нужный размер выборки или доверительный интервал
у вас есть. Оставьте поле Население пустым, если население очень велико или неизвестно.

Чтобы использовать этот мастер, введите частоты для одного слова
и размеры корпуса и нажмите кнопку расчета.

3

Примечания:
1. Введите простые числа без запятых.
(или другие нечисловые символы), так как они будут путать
калькулятор!

2. Мастер LL показывает знак плюс или минус перед значением логарифмической вероятности
чтобы указать чрезмерное или недостаточное использование соответственно в корпусе 1 по сравнению с корпусом 2.

3. Само значение логарифмического правдоподобия всегда является положительным числом. Однако мой сценарий сравнивает
относительные частоты между двумя корпусами, чтобы вставить индикатор для
«+» чрезмерное использование и «-» недостаточное использование корпуса 1 по сравнению с корпусом 2.

Корпус 1 Корпус 2
Частота слова
Размер корпуса

Как рассчитать логарифмическую вероятность

Логарифмическая вероятность рассчитывается путем построения таблицы непредвиденных обстоятельств следующим образом:

Corpus 1 Corpus 2 Total
Frequency of word a b a+b
Frequency of other words c-a d-b c+d-a-b
Итого c d c+d

Обратите внимание, что значение «c» соответствует количеству слов в корпусе.
один, а «d» соответствует количеству слов в корпусе два (N
ценности). Значения «a» и «b» называются наблюдаемыми значениями (O),
тогда как нам нужно рассчитать ожидаемые значения (E) в соответствии с
следующая формула:


В нашем случае N1 = c, а N2 = d. Итак, для этого слова E1 = c*(a+b) / (c+d)
и E2 = d*(a+b)/(c+d). Расчет ожидаемых значений занимает
учитывая размер двух корпусов, поэтому нам не нужно
нормализуйте цифры перед применением формулы. Мы можем тогда
рассчитать значение логарифмического правдоподобия по этой формуле:


Это равносильно вычислению логарифмической вероятности G2 следующим образом:
G2 = 2*((a*ln (a/E1)) + (b*ln (b/E2)))

Примечание 1: (спасибо Stefan Th. Gries) Форма логарифмического правдоподобия
Расчет, который я использую, взят из исследования Рида и Кресси, процитированного в
Rayson and Garside (2000), а не форму, полученную в Dunning (1993).

Примечание 2: (спасибо Крису Брю)
Чтобы сформировать логарифмическое правдоподобие, мы вычисляем сумму по членам формы
х*ln(х/Е). Для строго положительного x легко вычислить эти члены,
в то время как если x равно нулю, ln (x / E) будет отрицательной бесконечностью.
Однако предел
x * ln (x), когда x стремится к нулю, по-прежнему равно нулю, поэтому при суммировании мы можем просто
игнорировать ячейки, где x = 0.
Вычисление ln(0) возвращает ошибку, например,
MSExcel и библиотека C-math.

Чем выше значение G2, тем значительнее разница между
два показателя частоты. Для этих таблиц G2 равен 3,8 или выше.
значимо на уровне p

  • 95-й процентиль; 5% уровень; р 99-й процентиль; 1% уровень; р 99,9-й процентиль; уровень 0,1%; р 99,99-й процентиль; уровень 0,01%; п

    Расчет размера эффекта

    Наряду с мерой логарифмического правдоподобия на этой странице реализованы следующие меры размера эффекта:

    • %DIFF — см. Gabrielatos and Marchi (2012)
      Костас также предоставил FAQ с более подробной информацией.
    • Фактор Байеса (BIC) — см. Wilson (2013)
      Вы можете интерпретировать приблизительный коэффициент Байеса как степень доказательства против нулевой гипотезы следующим образом:
      0-2: не стоит большего, чем простое упоминание
      2-6 : положительное свидетельство против H0
      6-10: сильное свидетельство против H0
      > 10: очень сильное свидетельство против H0
      Для отрицательных оценок шкала читается как «за», а не «против» (Уилсон, личное сообщение).
    • Размер эффекта для логарифмического правдоподобия (ELL) — см. Johnston et al (2006)
      ELL варьируется от 0 до 1 (включительно). Джонстон и др. сказать, «интерпретация проста как пропорция максимального отклонения между
      наблюдаемые и ожидаемые пропорции».
    • Относительный риск — см. ссылки ниже
    • Log Ratio — см. CASS-блог Эндрю Харди, как интерпретировать это

      Обратите внимание, что если какое-либо слово имеет нулевую частоту, то автоматически применяется небольшая корректировка (0,5 наблюдаемой частоты
      который затем нормализуется), чтобы избежать ошибок деления на ноль.
    • Коэффициент шансов — см. ссылки ниже

    Дополнительная литература

    Для подробного сравнения логарифмической вероятности и статистики хи-квадрат см.
    Rayson P., Berridge D. and Francis B. (2004).
    Расширение правила Кокрана для сравнения частоты слов между корпусами.
    В томе II Purnelle G. , Fairon C., Dister A. (ред.)
    Le poids des mots: Материалы 7-й Международной конференции по
    Статистический анализ текстовых данных
    (JADT 2004), Лувен-ла-Нев, Бельгия, 10-12 марта 2004 г.     ,
    Presses universitaires de Louvain, стр. 926–936. ISBN 2-930344-50-4.

    • Логарифмический критерий правдоподобия можно использовать для сравнения корпусов. См.
    Rayson, P. and Garside, R. (2000).
    Сравнение корпусов с использованием частотного профилирования.
    В материалах семинара по
    Сравнивая корпуса,
    проводится в связи с 38-м ежегодным собранием Ассоциации компьютерной лингвистики
    (ACL 2000)     .
    1–8 октября 2000 г., Гонконг, стр. 1–6.

    Более подробный обзор различных статистических данных см.:
    Райсон, стр. (2003).
    Матрица: статистический метод и программный инструмент для лингвистического анализа посредством
    корпусное сравнение.
    к.т.н. диссертация , Ланкастерский университет.

    Чтобы узнать больше об использовании логарифмического правдоподобия при сравнении на уровне тегов, см. :
    Rayson, P. (2008).
    От ключевых слов к ключевым семантическим доменам.
    Международный журнал корпусной лингвистики .
    13:4 стр. 519-549.
    DOI: 10.1075/ijcl.13.4.06ray

    Калькулятор распределения хи-квадрат (Stat Trek)
    позволяет легко вычислить
    кумулятивные вероятности, основанные на статистике хи-квадрат.

    Аналогичный калькулятор есть в Институте фонетических наук в Амстердаме.

    См. также Даннинг, Тед. (1993).
    Точные методы статистики неожиданностей и совпадений.
    Компьютерная лингвистика , том 19, номер 1, стр. 61-74.
    (pdf)

    Эндрю Харди создал
    система проверки значимости
    который вычисляет хи-квадрат, логарифмическое правдоподобие и точный критерий Фишера
    для таблиц непредвиденных обстоятельств с использованием R.

    Растет движение в корпусной лингвистике и других областях.
    (например, психология)
    отказаться от проверки нулевой гипотезы и p-значений,
    и для расчета мер размера эффекта, а также значений значимости.
    Для обсуждения этих мер и зачем они нам нужны,
    см. следующие ресурсы,
    презентации и публикации:

    • CEP932 размер эффекта содержание
      в котором обсуждаются меры, включая d Коэна, коэффициент корреляции Пирсона r и отношение шансов.
    • Вацлав Брезина (2014) Размеры эффектов в корпусной лингвистике:
      ключевые слова, словосочетания и диахроническое сравнение.
      Представлено на конференции ICAME 2014, Ноттингемский университет.
      [Вацлав использует D Коэна в качестве меры размера эффекта.]
    • Величина эффекта для критерия хи-квадрат
      который описывает такие меры, как Phi, V Крамера,
      Отношение шансов и
      Относительный риск
    • Статистика для объяснения психологии
      Тестирование нулевой гипотезы и размеры эффекта, которые, например, утверждают
      «Если небольшое различие между средними значениями двух групп не является значимым, когда я тестирую 100 человек, должен ли я внезапно прийти в восторг от точно такой же разницы, если после тестирования 1000 человек я обнаружу, что теперь она значительна?»
    • Грис, Стефан Т. (2014)
      Таблицы частот, размеры эффектов и исследования.
      В Дилане Глинне и Джастине Робинсон (ред.), Корпусные методы семантики: количественные исследования полисемии и синонимии, 365–389.. Амстердам и Филадельфия: Джон Бенджаминс.
      [В этой статье Стефан использует показатели размера эффекта Phi, отношение шансов для таблиц 2 x 2 и V Крамера для больших таблиц r-by-c.]
    • Логарифмический коэффициент Эндрю Харди
      который на самом деле является двоичным журналом относительного риска и может применяться только к
      2 x 2 стола вместе с коэффициентом шансов.
    • Джонстон, Дж. Э., Берри, К. Дж. и Мильке, П.В. (2006)
      Меры размера эффекта для тестов согласия хи-квадрат и отношения правдоподобия.
      Перцептивные и моторные навыки: том 103, выпуск, стр. 412-414.
      DOI: 10.2466/pms.103.2.412-414
      [Это представляет меру размера эффекта, применимую к логарифмической вероятности.]
    • Кубергер А., Фриц А., Шерндль Т. (2014)
      Предвзятость публикации в психологии: диагноз, основанный на корреляции между размером эффекта и размером выборки.
      PLoS ONE 9(9): e105825. doi:10.1371/journal.pone.0105825
    • Джеффри Т. Лик и Роджер Д. Пэн (2015)
      Статистика: значения P — это только верхушка айсберга
      Nature 520, 612 (30 апреля 2015 г.) doi: 10.1038/520612a
      [Эта статья призывает нас не сосредотачиваться только на статистике: «Статистики и люди, которых они обучают и с которыми они сотрудничают, должны прекратить спорить о значениях P и не допустить, чтобы остальная часть айсберга пошла ко дну науки».]
    • Дональд Шарп (2015)
      Ваш критерий хи-квадрат статистически значим: что теперь?
      Практическая оценка, исследования и оценка. Том 20, номер 8, апрель 2015 г.
    • Блог Скотта Вайнгарта за 2013 г.
      Друзья не позволяют друзьям вычислять p-значения (без их полного понимания)
    • Блог и статья Шона Уоллиса о
      Меры ассоциации для таблиц непредвиденных обстоятельств
    • Камминг, Г. (2014)
      Новая статистика: почему и как.
      Психологическая наука. 25(1), стр. 7-29.
      DOI: 10.1177/0956797613504966
      [Упоминает, что D Коэна широко используется, но имеет подводные камни. ]
    • Габриэлятос, К. и Марчи, А. (2012)
      Keyness: Соответствующие показатели и практические вопросы.
      Международная конференция CADS 2012. Дискурсивные исследования с помощью корпуса: больше, чем сумма анализа дискурса и вычислений?, 13–14 сентября, Болонский университет, Италия.
      [Представляет меру размера эффекта %DIFF, которую, по мнению Костаса и Анны, следует применять к попарным сравнениям корпусов для расчета ключевости.]
    • Грис, Стефан Т. (2005)
      Проверка значимости нулевой гипотезы частоты слов: продолжение Килгарриффа.
      Корпусная лингвистика и лингвистическая теория 1(2). 277-294.
      [Стефан сравнивает хи-квадрат, p-значения, V Крамера, d Коэна и d*, а также
      Поправки Бонферрони и Холма для апостериорного тестирования.]

    Существует ряд других работ, связанных с использованием проверки значимости,
    статистика ключевости и сравнение корпусов, например.
    Килгаррифф (2005),
    Пако и Бестген (2009 г.)),
    Барон и др. (2009),
    Уилсон (2013)
    а также
    Лиффийт и др.

    Загружаемая электронная таблица

    Я сделал электронную таблицу, включающую расчет логарифмического правдоподобия и набор мер размера эффекта:
    SigEff. xlsx (последнее обновление: 4 июля 2016 г.). Это было бы полезно, если вы хотите рассчитать большой
    количество результатов из ранее существовавших наборов данных.
    Все размеры эффекта реализованы для случая 2 x 2, но только коэффициент Байеса и ELL реализованы для общего случая R x C,
    потому что %DIFF, относительный риск, логарифмическое отношение и отношение шансов применимы только к попарным сравнениям.

    Если у вас есть технические проблемы, пожалуйста, свяжитесь с
    Пол Рэйсон

    Найти доверительный интервал

     
    Уровень достоверности:

    95%
    99%

    Размер образца:
    Население:
    Процент:
    Доверительный интервал:

    Условия калькулятора размера выборки: доверительный интервал и доверительный уровень

    Доверительный интервал (также называемый пределом погрешности) представляет собой положительное или отрицательное значение, которое обычно сообщается в газетных или телевизионных результатах опросов общественного мнения. Например, если вы используете доверительный интервал 4 и 47 %, процент вашей выборки выбирает ответ, вы можете быть «уверены», что, если бы вы задали вопрос всей соответствующей совокупности, от 43 % (47-4) до 51 %. (47+4) выбрал бы этот ответ.

    Уровень достоверности говорит вам, насколько вы можете быть уверены. Он выражается в процентах и ​​показывает, как часто истинный процент населения, выбравшего ответ, находится в пределах доверительного интервала. 9Уровень достоверности 5% означает, что вы можете быть уверены на 95%; уровень достоверности 99% означает, что вы можете быть уверены на 99%. Большинство исследователей используют уровень достоверности 95%.

    Если сложить вместе доверительный интервал и доверительный интервал, можно сказать, что вы на 95 % уверены, что истинный процент населения находится в диапазоне от 43 % до 51 %. Чем шире доверительный интервал, который вы готовы принять, тем больше вы можете быть уверены, что ответы всей совокупности будут находиться в этом диапазоне.

    Например, если вы спросите выборку из 1000 человек в городе, какую марку колы они предпочитают, и 60% ответят, что бренд А, вы можете быть уверены, что от 40 до 80% всех людей в городе на самом деле предпочитают предпочитают эту марку, но вы не можете быть уверены, что между 59и 61% жителей города предпочитают этот бренд.

    Факторы, влияющие на доверительные интервалы

    Размер доверительного интервала для заданного уровня достоверности определяется тремя факторами:

    • Размер выборки
    • Процент
    • Численность населения

    Размер выборки

    Чем больше размер вашей выборки, тем больше вы можете быть уверены в том, что их ответы действительно отражают население. Это указывает на то, что для данного уровня достоверности, чем больше размер вашей выборки, тем меньше ваш доверительный интервал. Однако зависимость не является линейной ( т.е. , удвоение размера выборки не уменьшает вдвое доверительный интервал).

    Процент

    Ваша точность также зависит от процента вашей выборки, которая выбирает определенный ответ. Если 99 % вашей выборки ответили «Да», а 1 % — «Нет», шансы на ошибку минимальны, независимо от размера выборки. Однако, если проценты составляют 51% и 49%, вероятность ошибки намного выше. Легче быть уверенным в экстремальных ответах, чем в среднестатистических.

    При определении размера выборки, необходимого для данного уровня точности, вы должны использовать процент наихудшего случая (50%). Вы также должны использовать этот процент, если хотите определить общий уровень точности для уже имеющейся выборки. Чтобы определить доверительный интервал для определенного ответа, который дал ваш образец, вы можете использовать процент выбора этого ответа и получить меньший интервал.

    Численность населения

    Сколько человек входит в группу, которую представляет ваша выборка? Это может быть количество людей в городе, который вы изучаете, количество людей, которые покупают новые автомобили и т. д. Часто вы можете не знать точную численность населения. Это не является проблемой. Математика вероятности доказывает, что размер совокупности не имеет значения, если размер выборки не превышает нескольких процентов от общей совокупности, которую вы изучаете. Это означает, что выборка из 500 человек одинаково полезна для изучения мнений штата с населением 15 000 000 человек и города с населением 100 000 человек. По этой причине система опроса игнорирует размер популяции, когда он «большой» или неизвестен. Численность населения, вероятно, будет иметь значение только тогда, когда вы работаете с относительно небольшой и известной группой людей (9).0340 напр. , члены объединения).

    При расчете доверительного интервала предполагается, что у вас есть настоящая случайная выборка из соответствующей совокупности. Если ваша выборка не является действительно случайной, вы не можете полагаться на интервалы. Неслучайные выборки обычно являются результатом какого-либо недостатка или ограничения в процедуре выборки.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *