Расчет дома из оцилиндрованного бревна
масштаб чертежа 1:
0.250.511.5234
Укажите размеры
в миллиметрах
в сантиметрах
в метрах
Габариты стен
Длина стены фасада A
Длина боковой стены B
Размеры по габаритам
Размеры по осям
Высота фасада H
Высота боковой стены G
Высота стены сруба U
Длина перегородок 1 этажа L1
Высота перегородок 1 этажа P1
Длина перегородок 2 этажа L2
Высота перегородок 2 этажа P2
Размеры бревна
Диаметр бревна D
Высота C
Длина лапы T
Расстояние между нагелями N
Вес 1 кубического метра, кг V
Стоимость 1 кубического метра S
в цвете
черно-белый чертеж
Расчет материалов сруба из оцилиндрованного бревна
Укажите необходимые размеры стен.
A — Длина стены по фасаду.
B — Длина боковой стены.
Эти размеры можно указывать по внешним габаритам сруба или по осям стен. Вариант 1 или 2.
H — Высота фасада до конька фронтона. Если сруб без фронтона, то установите значение = 0
G — Высота боковой стены до конька фронтона. Если сруб без бокового фронтона, то установите значение = 0
U — Высота стены по углу.
T — Длина лапы.
Размеры оцилиндрованного бревна.
D — Диаметр бревна.
C — Полезная высота бревна, шаг одного венца. Размер должен быть обязательно меньше диаметра бревна.
Перегородки первого и второго этажей.
Укажите общую длину для всех перегородок первого этажа L1 и второго этажа L2.
Укажите высоту перегородок первого этажа P1 и второго этажа P2.
Если расчет перегородок сруба не требуется, то установите значения = 0
Дополнительные данные
N — Расстояние между нагелями.
V — Вес одного кубического метра оцилиндрованного бревна.
S — Ориентировочная стоимость одного кубического метра оцилиндрованного бревна.
Если высота стен основного сруба не кратно шагу венца, то программа изменит эту высоту.
В этом случае около результата появится сообщение Изменено!
Программа поможет рассчитать количество строительных материалов для строительства деревянного дома или бани из оцилиндрованного бревна.
Результат расчета содержит данные как по отдельности для стен, фронтонов и перегородок, так и их сумму.
Это периметр сруба, количество венцов, площади и объемы стен и перегородок, количество бревен и их общая длина.
Программа посчитает общий вес сруба и ориентировочную стоимость всего дома.
Площади наружных стен и перегородок будут полезны для расчета количества пропитки и покраски.
Общая длина бревен поможет рассчитать утеплитель между венцами.
Не забудьте учесть цену работы по сборке и монтажу, стоимость транспортировки.
Проемы, окна и двери не учитываются. На стоимость материалов они не влияют.
Количество нагелей расчитывается приблизительно.
Автор проекта: Дмитрий Житов © 2007 — 2022
FacebookVkontakte
Место приема благодарностей…
Автор: Бакуменко Валентина
Оцилиндрованное бревно
Дерево – уникальный природный строительный материал, обладающий большим количеством положительных свойств и имеющий огромное количество поклонников. Благодаря этому деревянные дома не утратили свою популярность даже после появления на рынке новых недорогих строительных материалов с хорошими качественными характеристиками. Более того, с началом применения фрезеровочных станков для оцилиндровки бревна и получения на выходе красивого, качественного и легкого в укладке материала кривая спроса на сооружения (дома, бани, дачи и пр. ) из дерева резко пошла вверх. Сегодня оцилиндрованное бревно распространено в строительстве не меньше, чем газосиликатные блоки, сэндвич-панели или кирпич.
) из дерева резко пошла вверх. Сегодня оцилиндрованное бревно распространено в строительстве не меньше, чем газосиликатные блоки, сэндвич-панели или кирпич.
Плюсы строительства из оцилиндрованного бревна
Природные характеристики оцилиндрованного бревна:
• Экологичность – дерево абсолютно безвредно для человека и не только не загрязняет атмосферу токсическими веществами, но и наоборот, оздоравливает микроклимат внутри помещения, дезинфицируя воздух при помощи фитонцидов, способных подавлять размножение бактерий и вирусов, а также улучшает самочувствие и настроение находящихся в помещении людей при помощи эфирных масел, выделяемых древесиной.
• Хорошие звукоизоляционные свойства – дерево само по себе плохо проводит тепло и звук, а качественные характеристики оцилиндрованных бревен и технология строительства домов из них позволяют минимизировать зазоры между бревнами в процессе кладки, ещё более улучшая качество шумоизоляции.
• Поддержание оптимального баланса влажности и температурного режима в помещении – микропористая структура древесины способствует естественному тепло- и воздухообмену, в результате чего в доме из оцилиндрованного бревна летом прохладно, зимой тепло, а воздух в нем никогда не становится спертым, сохраняя свежесть даже при закрытых окнах.
Технические характеристики оцилиндрованного бревна:
• Высокоточное производство – бревна обрабатываются станочным способом, вследствие чего имеют строго заданные параметры (диаметр, высота, длина).
• Замковая технология строительства – конструктивно оцилиндрованное бревно имеет специальные детали – пазы, с помощью которых происходит соединение брёвен в процессе кладки. Это делает возведение дома несложным и возможным (при строгом соблюдении технологии!) даже без участия профессиональных строителей.
• Привлекательный внешний вид – ровная поверхность, одинаковый размер оцилиндрованных бревен и природная красота дерева позволяют обходиться без внутренней и внешней декоративной отделки.
• Небольшой вес оцилиндрованного бревна – эта особенность дает возможность строить дома на «проблемных», мягкогрунтовых участках, а также экономить на фундаменте (такие дома можно смело ставить на недорогой монолитный ленточный мелкозаглубленный фундамент).
Минусы оцилиндрованного бревна
Как и у любого другого материала, у оцилиндрованного бревна есть свои минусы. Некоторые из них можно свести к минимуму или даже полностью устранить:
• Подверженность гниению и образованию плесени – устраняется путем нанесения биозащитной пропитки, работающей в качестве антисептика и уничтожающей микроорганизмы, способные вызывать гниение.
• Подверженность возгоранию – устраняется нанесением на поверхность материала антипирентов, которые, в случае возгорания и перехода огня на стены начинают выделять вещества, замедляющие и подавляющие горение.
• Относительно высокая стоимость – цена дома из оцилиндрованного бревна выше стоимости дома из газосиликатных блоков или панельного дома. Однако качественные характеристики и срок службы дома с лихвой перекрывают недостатки цены.
• Длительность сроков возведения дома – в связи с тем, что дерево сильно усаживается, смонтированный сруб должен отстояться по меньшей мере полгода прежде, чем можно будет продолжить строительство. Это единственный минус оцилиндрованного бревна (и в целом дерева как строительного материала), который не поддаётся коррекции, так как нарушение технологии строительства может повлечь довольно неприятные и даже опасные последствия.
Это единственный минус оцилиндрованного бревна (и в целом дерева как строительного материала), который не поддаётся коррекции, так как нарушение технологии строительства может повлечь довольно неприятные и даже опасные последствия.
Расчет количества материала
Как я уже говорила, высокая стоимость оцилиндрованного бревна является одним из его минусов. Она практически сравнима со стоимостью кирпича – самого дорогого строительного материала. Поэтому, прежде чем решиться на строительство дома из оцилиндровки, необходимо произвести предварительные расчеты количества бревна, которое понадобится для его возведения.
В расчётах вы можете использовать наш строительный калькулятор. Для этого не обязательно иметь уже готовый рабочий проект, однако необходимо знать параметры бревна, из которого вы собираетесь строить (диаметр, высоту, длину лапы), вес и стоимость его кубометра, а также иметь приблизительное представление о размерах будущего дома. Хотя наличие плана, разумеется, будет огромным плюсом, так как чем точнее выставляются начальные параметры, тем точнее будет произведён расчет.
Наша бесплатная программа для расчета количества оцилиндрованного бревна, требуемого для строительства дома, дачи или бани, выводит в итоговом окне не только количество и примерную стоимость готового сруба, но и размер площадей стен, общей площади сооружения, периметр дома, количество венцов и иные параметры.
Также программа выведет схематические изображения фасада, боковой стены дома, дома в плане и самого бревна – каждое с числовым указанием заложенных и полученных размеров. Отдельно будут даны параметры перегородок этажей и общие размеры, объемы, длины и вес всех элементов будущего дома.
В тех местах, где программа была вынуждена изменить начальные значения, об этом будет красным шрифтом выведено предупреждение.
Все представленные в итоговом расчете сведения будут полезны как для подсчета необходимого количества оцилиндрованного бревна, так и для примерного расчёта необходимого количества огне- и биозащитных пропиток, а также утеплителя, который потребуется в дальнейшем для конопачения пазов и межвенцовых щелей дома.
Читайте так же о том, как выбрать и хранить оцилиндрованное бревно.
Кубатурник оцилиндрованного бревна
Главная
Строительство
Кубатурник бревна: как рассчитать объем оцилиндрованных бревен
Оцилиндрованные бревна — идеальный материал для строительства бани или загородного дома. Такие изделия отличает экологичность и безопасность, привлекательный внешний вид и быстрый монтаж, легкость в установке и обработке. За счет специальной технологии изготовления бревна обретают идеально ровную цилиндрическую форму и гладкую поверхность, одинаковые диаметры и размеры.
Благодаря этим параметрам изделия укладываются вплотную, что исключает появление трещи в срубе. Кроме того, возведение дома или бани происходит легко и оперативно. Бревенчатое строение будет выглядеть изящно и аккуратно.
10 причин строить дом из оцилиндрованных бревен
- Натуральная и экологически чистая древесина не выделяет токсичных веществ и безопасна для человека.
 Более того, дерево обладает целебными свойствами и благоприятно влияет на самочувствие и сон человека;
Более того, дерево обладает целебными свойствами и благоприятно влияет на самочувствие и сон человека; - Древесина способствует быстрому воздухообмену и обновляет кислород до 30% в сутки. Поэтому в деревянном доме всегда комфортно находится и легко дышать;
- Привлекательный и эстетичный внешний вид. Бревенчатый дом выглядит изысканно и естественно. Он гармонично впишется в любой пейзаж и будет выгодно выделяться на фоне других построек;
- За счет специальной обработки материала на станках, бревна получают ровную и гладкую поверхность. Поэтому изделия плотно прилегают друг к другу и исключают появления зазоров в стенах;
- Одинаковые диаметры и размеры бревен ускоряют и упрощают монтаж. В зависимости от сложности проекта установка сруба займет всего от 3-5 дней до 3-4 недель!;
- Легкий вес древесины не потребует массивного и дорогостоящего фундамента;
- Оцилиндрованное бревно не требует декоративной отделки ни внутри, ни снаружи здания. Кстати, отделка “под ноль” в бревенчатом доме смотрится гармонично и эффектно;
- Древесина имеет высокие тепло- и звукоизоляционные показатели.
 В бревенчатом доме тепло, тихо и спокойно;
В бревенчатом доме тепло, тихо и спокойно; - При правильной конопатке сруба, не потребуется повторной процедуры. Тогда как дома из бруса обязательна нужна повторная конопатка после усадки;
- Бревна легко поддаются обработке, что позволяет создавать интересные конструкции (дома с эркером, резными балконами, верандами в виде ротонды и пр.). Кроме того, бревенчатый дом может быть построен в любом стиле!
Как рассчитать объемы материалов
Тем, кто решил строить бревенчатый дом, важно правильно рассчитать необходимое количество строительных материалов. Так как бревна характеризует цилиндрическая форма, проводить расчет нужно исходя из этого параметра. Нельзя рассчитать объем, просто умножив толщину стен на высоту. Чтобы правильно сделать самостоятельно используют специальный кубатурник оцилиндрованного бревна.
Самый простой расчет проводят по формуле = П*R2*Н, где
П = 3,14;
R2 — радиус оцилиндрованного бревна в квадрате;
Н — длина оцилиндрованного бревна.
Полученный результат умножаем на количество необходимых бревен для строительства дома или бани. Не забывайте прибавить и 7%, которые выделяют на усадку бревенчатого сруба. Чтобы облегчить расчет, результаты для разных диаметров бревен представляет таблица кубатуры бревна.
Таблица кубатуры оцилиндрованного бревна длиной 6 метров
| Диаметр, мм | Высота, мм | Объем, м3 | Площадь, м2 | Количество в м3, шт |
| 140 | 130,6 | 0,09 | 1,453 | 11,1 |
| 160 | 149,2 | 0,12 | 1,662 | 8,29 |
| 180 | 167,9 | 0,15 | 1,869 | 6,55 |
| 200 | 186,6 | 0,19 | 2,078 | 5,31 |
| 220 | 205,2 | 0,23 | 2,286 | 4,39 |
| 240 | 223,9 | 0,27 | 2,493 | 3,69 |
| 260 | 242,5 | 0,32 | 2,701 | 3,14 |
| 280 | 261,2 | 0,37 | 2,908 | 2,71 |
| 300 | 279,9 | 0,42 | 3,117 | 2,36 |
| 320 | 298,5 | 0,48 | 3,325 | 2,07 |
| 340 | 317,2 | 0,54 | 3,532 | 1,84 |
| 360 | 335,8 | 0,61 | 3,74 | 1,64 |
На объем и стоимость материалов влияет не только порода древесины, но и диаметры бревна. Если вы планируете строительство дома для постоянного проживания, выбирайте размеры не менее 240 мм, а для северных регионов — более 260 мм. Если это будет летний дачный домик для сезонного проживания и отдыха, подойдут бревна диаметром 220 мм. Для беседки можно взять минимальные размеры.
Если вы планируете строительство дома для постоянного проживания, выбирайте размеры не менее 240 мм, а для северных регионов — более 260 мм. Если это будет летний дачный домик для сезонного проживания и отдыха, подойдут бревна диаметром 220 мм. Для беседки можно взять минимальные размеры.
Таблица — не единственный способ рассчитать нужное количество стройматериалов. Существует специальный онлайн калькулятор, который произведет быстрый и точный расчет количества и стоимости материалов с учетом усадки, внутренних перегородок и других факторов.
Кроме того, калькулятор рассчитает полезную площадь помещения, количество венцов и нагрузку на фундамент. Как правило, на сайтах строительных компаний каждый типовой проект сопровождает свой калькулятор.
Если вы не знаете, как правильно рассчитать кубатуру бревен, Вам помогут специалисты компании “МариСруб”! Опытные мастера подберут и рассчитают объем материалов. Эксперты рекомендуют брать выбирать оцилиндрованные бревна из сосны, так как это лучшее соотношение цена-качество.
Сосна — доступная крепкая древесина, которую отличает прочность и долговечность, приятный хвойный аромат и красивая фактурой. Выбирайте понравившийся вариант бревенчатого дома или заказывайте индивидуальный проект! Специалисты бесплатно подготовят смету будущего дома или дачи, рассчитают объем материалов и стоимость строительства.
Логарифм | Правила, примеры и формулы
- Ключевые люди:
- Джон Напье
Генри Бриггс
Йоост Бюрги
- Похожие темы:
- натуральный логарифм
мантисса
десятичный логарифм
сила
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
логарифм , показатель или степень, в которую необходимо возвести основание, чтобы получить данное число. Выражаясь математически, x — это логарифм N до базы B , если B x = N , в этом случае один из них пишет x = log B . Например, 2 3 = 8; следовательно, 3 — это логарифм 8 по основанию 2, или 3 = log 2 8. Таким же образом, поскольку 10 2 = 100, то 2 = log 10 100. Логарифмы последнего вида (что логарифмы с основанием 10) называются обычными или бриггсовскими логарифмами и записываются просто log п .
Например, 2 3 = 8; следовательно, 3 — это логарифм 8 по основанию 2, или 3 = log 2 8. Таким же образом, поскольку 10 2 = 100, то 2 = log 10 100. Логарифмы последнего вида (что логарифмы с основанием 10) называются обычными или бриггсовскими логарифмами и записываются просто log п .
Логарифмы, изобретенные в 17 веке для ускорения вычислений, значительно сократили время, необходимое для умножения многозначных чисел. Они были основными в численной работе более 300 лет, пока совершенствование механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделало их устаревшими для крупномасштабных вычислений. Натуральный логарифм (с основанием e ≅ 2,71828 и записанный как ln n ), однако, продолжает оставаться одной из самых полезных функций в математике, с приложениями к математическим моделям во всех физических и биологических науках.
Свойства логарифмов
Логарифмы были быстро приняты учеными из-за различных полезных свойств, которые упрощали долгие и утомительные вычисления. В частности, ученые могли найти произведение двух чисел m и n , просматривая логарифм каждого числа в специальной таблице, складывая логарифмы вместе, а затем снова обращаясь к таблице, чтобы найти число с этим вычисленным логарифмом (известным как его антилогарифм). Выраженная в виде десятичных логарифмов, эта связь определяется как log m n = log m + log n . Например, 100 × 1000 можно вычислить, найдя логарифмы 100 (2) и 1000 (3), сложив логарифмы (5), а затем найдя антилогарифм (100 000) в таблице. Точно так же задачи деления преобразуются в задачи вычитания с логарифмами: log m / n = log m − log n . Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также можно преобразовывать между любыми положительными основаниями (за исключением того, что 1 нельзя использовать в качестве основания, поскольку все его степени равны 1), как показано в Щелкните здесь, чтобы увидеть полноразмерную таблицу логарифмических законов.
В частности, ученые могли найти произведение двух чисел m и n , просматривая логарифм каждого числа в специальной таблице, складывая логарифмы вместе, а затем снова обращаясь к таблице, чтобы найти число с этим вычисленным логарифмом (известным как его антилогарифм). Выраженная в виде десятичных логарифмов, эта связь определяется как log m n = log m + log n . Например, 100 × 1000 можно вычислить, найдя логарифмы 100 (2) и 1000 (3), сложив логарифмы (5), а затем найдя антилогарифм (100 000) в таблице. Точно так же задачи деления преобразуются в задачи вычитания с логарифмами: log m / n = log m − log n . Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также можно преобразовывать между любыми положительными основаниями (за исключением того, что 1 нельзя использовать в качестве основания, поскольку все его степени равны 1), как показано в Щелкните здесь, чтобы увидеть полноразмерную таблицу логарифмических законов.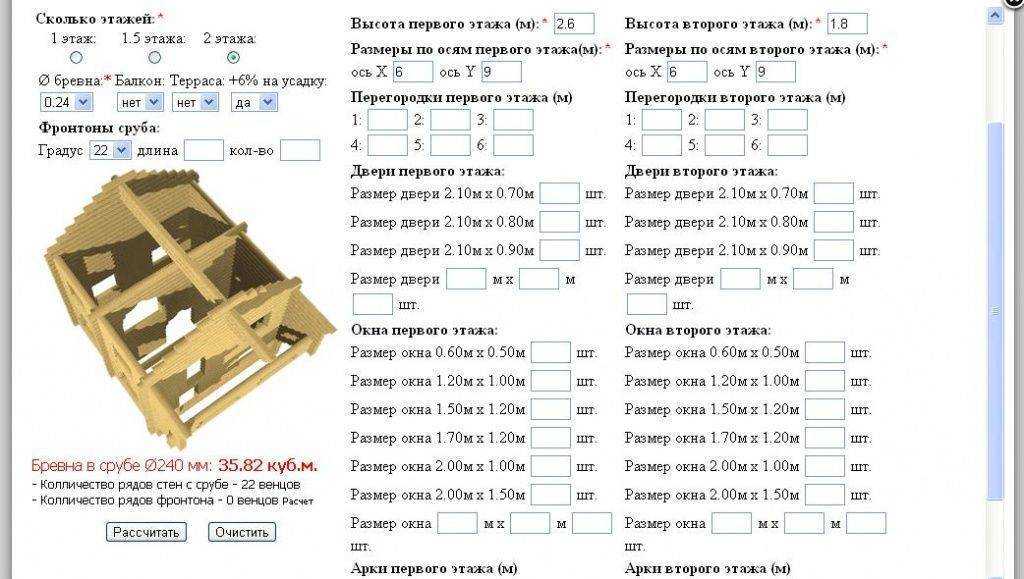
Обычно в таблицы логарифмов включались только логарифмы чисел от 0 до 10. Чтобы получить логарифм некоторого числа за пределами этого диапазона, число сначала было записано в научной записи как произведение его значащих цифр и его экспоненциальной степени — например, 358 будет записано как 3,58 × 10 2 , а 0,0046 будет можно записать как 4,6 × 10 −3 . Затем в таблице можно было найти логарифм значащих цифр — десятичную дробь от 0 до 1, известную как мантисса. Например, чтобы найти логарифм числа 358, нужно найти log 3,58 ≅ 0,55388. Следовательно, log 358 = log 3,58 + log 100 = 0,55388 + 2 = 2,55388. В примере числа с отрицательным показателем степени, например 0,0046, можно найти log 4,6 ≅ 0,66276. Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = -2,33724.
История логарифмов
Изобретение логарифмов было предвосхищено сравнением арифметических и геометрических последовательностей. В геометрической последовательности каждый член образует постоянное отношение со своим последующим; Например,
…1/1000, 1/100, 1/10, 1, 10, 100, 1000…
имеет обыкновенное отношение 10. В арифметической последовательности каждый последующий член отличается на константу, известную как общая разность; Например,
В арифметической последовательности каждый последующий член отличается на константу, известную как общая разность; Например,
…−3, −2, −1, 0, 1, 2, 3…
имеет общую разность, равную 1. Обратите внимание, что геометрическую последовательность можно записать в терминах ее общего отношения; для приведенного выше примера геометрической последовательности:
…10 −3 , 10 −2 , 10 −1 , 10 0 , 10 1 , 10 2 , 10 3 … .
Умножение двух чисел в геометрической последовательности, скажем, 1/10 и 100, равносильно сложению соответствующих показателей степени обыкновенного отношения, -1 и 2, чтобы получить 10 1 = 10. Таким образом, умножение превращается в сложение. Однако первоначальное сравнение двух серий не было основано на каком-либо явном использовании экспоненциальной записи; это была более поздняя разработка. В 1620 г. швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции соотношения геометрических и арифметических последовательностей.
Шотландский математик Джон Нейпир опубликовал свое открытие логарифмов в 1614 году. Его цель состояла в том, чтобы помочь в умножении величин, которые тогда назывались синусами. Весь синус был величиной стороны прямоугольного треугольника с большой гипотенузой. (Первоначальная гипотенуза Непера была 10 7 .) Его определение было дано в терминах относительных скоростей.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Таким образом, логарифм любого синуса представляет собой число, очень точно выражающее линию, которая одинаково увеличивалась в течение определенного времени, в то время как линия всего синуса пропорционально уменьшалась в этом синусе, причем оба движения были равновременны и начало смещалось одинаково.
В сотрудничестве с английским математиком Генри Бриггсом Нейпир привел свой логарифм в его современную форму. Для логарифма Напера сравнение будет между точками, движущимися по градуированной прямой линии, L точка (для логарифма) движется равномерно от минус бесконечности до плюс бесконечности, X точка (для синуса) движется от нуля до бесконечности со скоростью, пропорциональной ее расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице, и их скорости в этой точке равны. Суть открытия Непера состоит в том, что оно представляет собой обобщение отношения между арифметическим и геометрическим рядами; т. е. умножение и возведение в степень значений 9Точка 0023 X соответствует сложению и умножению значений точки L соответственно. На практике удобно ограничить движение L и X требованием, чтобы L = 1 при X = 10 в дополнение к условию, что X = 1 при L = 0. Это изменение привело к бриггсовскому или десятичному логарифму.
Кроме того, L равно нулю, когда X равно единице, и их скорости в этой точке равны. Суть открытия Непера состоит в том, что оно представляет собой обобщение отношения между арифметическим и геометрическим рядами; т. е. умножение и возведение в степень значений 9Точка 0023 X соответствует сложению и умножению значений точки L соответственно. На практике удобно ограничить движение L и X требованием, чтобы L = 1 при X = 10 в дополнение к условию, что X = 1 при L = 0. Это изменение привело к бриггсовскому или десятичному логарифму.
Нейпир умер в 1617 году, и Бриггс продолжил работу в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанных до 14 знаков после запятой для чисел от 1 до 20 000 и от 9.от 0 000 до 100 000. В 1628 году голландский издатель Адриан Влак опубликовал 10-местную таблицу для значений от 1 до 100 000, добавив недостающие 70 000 значений. И Бриггс, и Влак занимались созданием логарифмических тригонометрических таблиц. Такие ранние таблицы были либо с точностью до одной сотой градуса, либо с точностью до одной угловой минуты. В 18 веке таблицы были опубликованы для 10-секундных интервалов, которые были удобны для таблиц с семью десятичными знаками. В общем случае требуются более тонкие интервалы для вычисления логарифмических функций меньших чисел, например, при вычислении функций log sin x и логарифмический тангенс x .
Такие ранние таблицы были либо с точностью до одной сотой градуса, либо с точностью до одной угловой минуты. В 18 веке таблицы были опубликованы для 10-секундных интервалов, которые были удобны для таблиц с семью десятичными знаками. В общем случае требуются более тонкие интервалы для вычисления логарифмических функций меньших чисел, например, при вычислении функций log sin x и логарифмический тангенс x .
Наличие логарифмов сильно повлияло на форму плоской и сферической тригонометрии. Процедуры тригонометрии были переработаны для получения формул, в которых операции, зависящие от логарифмов, выполняются одновременно. Тогда обращение к таблицам состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов.
Фрэнсис Дж. Мюррей
Как считать логарифмы — World Mental Calculation 93 = 1000\), поэтому \(\log 1000 = 3\)
Они обычно используются в математике, но редко используются при вычислениях в уме. Однако описанный здесь метод используется для метода вычисления сложных корней и степеней.
Однако описанный здесь метод используется для метода вычисления сложных корней и степеней.
Математика:
Математики узнают, что всегда верно следующее:
- \(\log (a*b) = \log a + \log b\)
- \(\log (\frac{a}{b}) = \log a – \log b\)
Следовательно, если мы знаем приблизительные значения \(\log 2 = 0,30103\) и \(\log 3 = 0,47712\), мы можем вычислить следующие примеры:
- \(\log{20} = \log{10 } + \log{2} = 1 + 0,30103 = 1,30103\)
- \(\log{6} = \log{2} + \log{3} = 0,30103 + 0,47712 = 0,77815\)
- \(\log{32} = 5 * \log{2} = 5 * 0,30103 = 1,50515\)
- \(\log{2.5} = \log{10} – 2 * \log{2} = 1 – 2 * 0,30103 = 0,39794\)
Наш метод вычисления логарифмов основан на запоминании различных значений логарифмов и их объединении для нахождения значения требуемого логарифма.
Подготовка:
Выучите следующие значения логарифмов – и, возможно, больше:
\(\log 2 = 0,30103\)
\(\log 3 = 0,47712\)
\(\log 7 )
\(\log 1,1 = 0,04139\)
\(\log 1,3 = 0,11394\)
\(\log 1,7 = 0,23045\)
\((\log 1,019 1 ) 0,004020 0,004020 Метод:
- Выберите число, очень близкое к исходному числу, которое вы можете построить, используя множители, логарифмы которых вы выучили.

 Более того, дерево обладает целебными свойствами и благоприятно влияет на самочувствие и сон человека;
Более того, дерево обладает целебными свойствами и благоприятно влияет на самочувствие и сон человека; В бревенчатом доме тепло, тихо и спокойно;
В бревенчатом доме тепло, тихо и спокойно;