Что такое кубические единицы? Определение, формула, объем, примеры
Что такое кубическая единица?
Кубическая единица — это единица измерения объема.
Другими словами, эти единицы являются способом измерения пространства, занимаемого чем-либо.
Подумайте о книге: Каков ее объем? Его объем зависит от длины, ширины и высоты. Умножение этих трех линейных измерений дает нам кубическое измерение.
Объем относится к пространству, занимаемому объектом или трехмерной фигурой. Измеряется в кубических единицах.
Точно так же объем воды в бассейне можно измерить в кубических единицах.
Рекомендуемые рабочие листы:
Определение кубических единиц
В геометрии кубические единицы могут быть определены как единицы, используемые для измерения объема. Объем единичного куба, длина, ширина и высота которого равны 1 единице, равен 1 кубической единице.
Символ кубических единиц может быть указан как единица 3 .
Например, «кубический сантиметр» можно представить как см 3 .
Обычные единицы измерения, такие как дюймы, футы, ярды, мили, сантиметры, метры и километры, описывают стороны фигуры, как стороны прямоугольника. Кубические единицы измеряют трехмерное пространство или объем.
Как работает кубическая единица?
Каждое измерение куба единиц (длина, ширина и высота) является одной единицей.
Итак, одна единица длины с одной единицей ширины и одной единицей высоты вместе составляют объем одной кубической единицы .
Когда мы измеряем объем, мы измеряем его с точки зрения того, сколько «единичных кубов» по 1 кубической единице объема каждый поместится в этом объеме, если мы поместим их рядом или один поверх другого.
На изображении ниже мы можем найти объем данной фигуры, подсчитав общее количество кубических единиц. Он состоит из $10 \times 10$ кубических единиц. Значит объем фигуры 100 кубических единиц.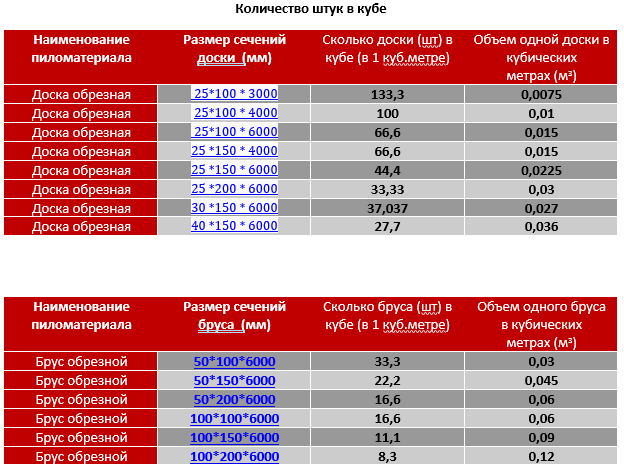
При расчете объема чего-либо в кубических единицах вы должны умножить значение каждого измерения (длина, ширина и высота).
Длина, ширина и высота измеряются в отдельных единицах, таких как дюймы, футы и ярды или сантиметры и метры.
Например, на приведенном ниже рисунке прямоугольный параллелепипед состоит из меньших единичных кубов. Кубоид имеет длину 6 дюймов, высоту 4 дюйма и ширину 2 дюйма.
При перемножении размеров получается объем, выраженный в кубических единицах (таких как кубические дюймы, кубические футы, кубические ярды, кубические сантиметры или кубические метры).
Умножение размеров прямоугольного параллелепипеда:
$6$ $\text{дюймы} \times 4$ $\text{дюймы} \times 2$ $\text{дюймы} = 48$ $\text{кубические дюймы}$
48 кубических дюймов — это объем в кубических единицах.
Длину, ширину и высоту прямоугольного параллелепипеда также можно измерить, подсчитав количество единичных кубов. Затем объем определяется в кубических единицах.
Попробуем другой пример. Если сторона куба 5 дм, то каков будет его объем?
Объем куба $= \text{length} \times \text{width} \times \text{height}$
Поскольку длина, ширина и высота в кубе равны, объем будет:
$5 \times 5 \times 5 = 125$ кубических дюймов.
Мы видим, что единица измерения дюймов меняется на кубические дюймы.
Некоторыми примерами кубических единиц в метрических единицах являются кубические метры и кубические сантиметры, а в обычных единицах измерения — кубические дюймы и кубические футы.
Такие единицы, как квадратные дюймы, квадратные футы, квадратные ярды, квадратные мили, квадратные сантиметры, квадратные метры и квадратные километры, описывают площадь фигуры и используются для измерения двумерных фигур или площадей.
Кубические единицы, такие как кубические дюймы, кубические футы, кубические сантиметры и кубические метры, измеряют трехмерное пространство или объем.
Кубические преобразования
Мы можем преобразовать одну кубическую единицу (например, кубические дюймы) в другую кубическую единицу (например, кубические футы).
Некоторые приблизительные преобразования для кубических единиц приведены ниже:
1 кубический дюйм $ = 0,0006 $ кубических футов
1 кубический дюйм $ = 0,00002 $ кубических ярдов
1 кубический дюйм $ = 16,39 $ кубических сантиметров
1 кубический дюйм $= 0,000016$ кубических метров
1 кубический фут $= 1728$ кубических дюймов
1 кубический фут $= 0,037$ кубических ярдов
1 кубический фут $= 28316,85$ кубических футов 1 $
7 = 0,028$ кубических метров
1 кубический сантиметр $= 0,000001$ кубических метров
1 кубический сантиметр $= 0,061$ кубических дюймов
1 кубический сантиметр $= 0,000035$ куб.
1 кубический метр $ = 1 000 000 $ кубических сантиметров
1 кубический метр $= 61023,7$ кубических дюймов
1 кубический метр $= 35,3$ кубических футов
1 кубический метр $= 1,31$ кубических ярдов
Решаемые примеры
1. Сколько стоит каждая сторона единицы кубическая мера?
Раствор : 1 шт.
Единичный куб имеет длину, ширину и высоту, равные одной единице.
2. Книга имеет длину 12 дюймов, ширину 10 дюймов и высоту 4 дюйма. Каков его объем?
Решение : Объем книги $= \text{длина} \times \text{ширина} \times \text{высота}$
$= 12$ $\text{дюймов} \times 10$ $\text {inches} \times 4$ $\text{inches}$
$= 480$ кубических дюймов
Объем книги 480 кубических дюймов.
3. Сколько кубических дюймов составляет один кубический фут?
Решение : 1 фут $= 12$ дюймов
1 кубический фут $= 1$ $\text{фут} \times 1$ $\text{фут} \times 1$ $\text{фут}$
Таким образом, 1 кубический фут $= 12$ $\text{дюймы} \times 12$ $\text{дюймы} \times 12$ $\text{дюймы}$
$= 1728$ кубические дюймы
Практические задачи
1
Сколько кубических футов составляет один кубический ярд?
3 кубических фута
10 кубических футов
27 кубических футов
9 кубических футов
Правильный ответ: 27 кубических футов
1 ярд $= 3$ футов
1 кубический ярд $= 3$ $\text{футы } \times 3$ $\text{футы} \times 3$ $\text{футы}$
$= 27$ кубических футов
2
Каков объем пол-литра молока?
5000 мл
500 кубических метров
0,005 кубические метры
0,0005 кубические метры
Правильный ответ: 0,0005 кубических метров
1 кубический метр $ = 1000 $ Liters
SO 1 литр $ 0,001 $ Cubic Metters
7 $ Litters
SO 1 литр $ 0,001 $ Кубические метры
777 $
SO 1 -лит.
0,5 литра $= 0,0005$ кубических метров
3
Классная комната имеет длину 10 ярдов, ширину 8 ярдов и высоту 6 ярдов. Каков объем класса?
60 куб. ярдов
80 куб. ярдов
480 куб. ярдов
480 ярдов
Правильный ответ: 480 куб. text{yards} \times 6$ $\text{yards}$
$= 480$ кубических ярдов
4
Сторона кубического ящика равна 0,5 фута. Вычислите объем в кубических футах.
0,25 куб. фута
0,125 куб. фута
1,25 куб. фута
12,5 куб. фута
Правильный ответ: 0,125 кубических фута
Поскольку это кубическая коробка, длина, ширина и высота равны, поэтому все они равны 0,5 фута.
Объем кубического ящика $= 0,5$ $\text{футы} \times 0,5$ $\text{футы} \times 0,5$ $\text{футы}$
$= 0,125$ кубические футы
Часто задаваемые вопросы
Почему важны кубические единицы?
Кубические единицы важны, потому что они представляют стандартные единицы объема.
Это помогает нам измерять объем в разных единицах, таких как кубические дюймы или кубические сантиметры.
Можем ли мы использовать кубические единицы для измерения объема трехмерных фигур, отличных от куба?
Да, кубические единицы можно использовать для измерения объема различных трехмерных фигур, таких как сфера, прямоугольный параллелепипед или призма.
Кубические единицы используются для измерения общего занимаемого пространства, поэтому форма фигуры не имеет значения.
Можно ли использовать кубические единицы для измерения объема жидкостей?
Да, мы можем использовать кубические единицы для измерения объема жидкостей.
Мы делаем это путем преобразования единиц объема жидкости, таких как литры или мл, в кубические единицы, такие как кубические метры.
Калорий в кубике сахара
Крупный план кубиков сахара.
Изображение предоставлено:
lnmark/iStock/Getty Images
Некоторые сахара неизбежны.
Фруктоза во фруктах, мальтоза в зернах или даже лактоза в молоке — это встречающиеся в природе сахара, которые обычно не вызывают большого беспокойства в вашем рационе — эти продукты содержат другие питательные вещества. Но кубик сахара не дает ничего, кроме глюкозы и, следовательно, калорий для энергии. Несмотря на то, что натуральный сахар содержит такое же количество калорий, как и сахар-песок из кусочка сахара, грамм за граммом, добавленный сахар — это не то, что вам нужно в своем рационе.
Сахар и калории
На каждый грамм сахара в еде вы получите 4 калории. Один кубик сахара весит 2,3 грамма и содержит примерно 9 калорий. Все виды сахара имеют одинаковое количество калорий. Независимо от того, едите ли вы кубик сахарного песка, меда, кукурузного сиропа, декстрозы, мальтозы или других видов сахара, количество калорий на грамм одинаково.
Видео дня
Сколько вы можете иметь
Слишком много сахара в вашем рационе может привести к увеличению веса, что повышает вероятность развития хронических заболеваний.
Это добавленный сахар из обработанных пищевых продуктов, однако это является серьезной проблемой, потому что эти нездоровые продукты предлагают минимальное количество питательных веществ. Ограничьте себя не более чем 100 калориями из добавленных сахаров в день, что составляет около 25 граммов, если вы женщина. Не более 150 калорий в вашем рационе — 38 граммов — должны поступать из добавленных сахаров, если вы мужчина, предполагает Американская кардиологическая ассоциация. В зависимости от того, к какой группе вы относитесь, всего на один кубик сахара приходится от 6 до 10 процентов дневной нормы добавленного сахара.
Углеводы
Все виды сахара, добавленного или натурального, являются углеводами. Поэтому, если вы решите съесть лакомство с добавлением сахара, вам придется учитывать это в общем потреблении углеводов. От 45 до 65 процентов калорий в вашем рационе должны поступать из углеводов, как указано в публикации «Диетические рекомендации для американцев, 2010».
Если 2000 — это среднее суточное количество калорий, вам потребуется от 900 до 1300 калорий из углеводов, или от 225 до 325 граммов. Если вы кладете всего один кубик сахара в свой утренний кофе, он потребляет менее 1 процента вашей дневной нормы углеводов. Но это пустые калории, так как из сахара вы не получите ни клетчатки, ни витаминов, ни минералов.
Сведения о гликемическом индексе
Несмотря на то, что все виды сахара имеют одинаковую калорийность, не все они одинаково влияют на уровень сахара в крови. Большинство продуктов, содержащих углеводы, имеют рейтинг гликемического индекса, или ГИ, который оценивает продукты в зависимости от того, насколько быстро они повышают уровень сахара в крови. Продукты с показателем выше 70 могут быстро поднять уровень сахара в крови. Продукты со средним гликемическим индексом имеют рейтинг от 55 до 70, в то время как продукты с низким гликемическим индексом имеют рейтинг менее 55 и постепенно повышают уровень сахара в крови.